
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 若 ![]() , 求
, 求 ![]() 的值.
的值.
(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,
CG和EH的数量关系是 , ![]() 的值是 .
的值是 .
(2)类比延伸:如图2,在原题条件下,若 ![]() (m>0)则
(m>0)则 ![]() 的值是(用含有m的代数式表示),试写出解答过程 .
的值是(用含有m的代数式表示),试写出解答过程 .
(3)拓展迁移:如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若 ![]() (a>0,b>0)则
(a>0,b>0)则 ![]() 的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示).
【答案】
(1)AB=3EH,CG=2EH,![]()
(2)解: ![]() ,如下图所示,作EH∥AB交BG于点H,
,如下图所示,作EH∥AB交BG于点H,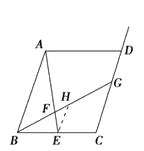 则△EFH∽△AFB∴
则△EFH∽△AFB∴ ![]() =
= ![]() =m,∴AB=mEH∵?ABCD∴AB=CD=mEH∵EH∥AB∥CD∴△BEH∽△BCG∴
=m,∴AB=mEH∵?ABCD∴AB=CD=mEH∵EH∥AB∥CD∴△BEH∽△BCG∴ ![]() =
= ![]() =2,∴CG=2EH,∴
=2,∴CG=2EH,∴ ![]() =
= ![]() =
= ![]()
(3)ab+1
【解析】解:(1)依题意,过点E作EH∥AB交BG于点H,如图下图所示,

则有△ABF∽△EHF,
∴ ![]() =
= ![]() =3,
=3,
∴AB=3EH,
∵ABCD,EH∥AB
∴EH∥CD
又∵E为BC的中点,
∴EH为△BCG的中位线,
∴CG=2EH,∴ ![]() ,
,
( 3 )如下图示,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD

∵EH∥CD
∴△BCD∽△BEH,∴ ![]() =
= ![]() =b,∴CD=bEH
=b,∴CD=bEH
又 ![]() =a,
=a,
∴AB=aCD=abEH,∵EH∥AB,∴△ABF∽△EHF,
∴ ![]() ∴
∴ ![]() .
.
(1)本小题体现“特殊”的情形是一个确定值,添加辅助线过点E作EH∥AB交BG于点H,易证△ABF∽△EHF,相似三角形的对应边成比例,即可求出AB和EH的数量关系,再证明EH为△BCG的中位线,就可以得出CG和EH的数量关系,![]() =
=![]() ,即可求出结果。
,即可求出结果。
(2)本小题体现“一般”的情形,首先作EH∥AB交BG于点H,证明△EFH∽△AFB,从而得出AB与EH的数量关系,然后根据EH∥AB∥CD,证得△BEH∽△BCG,得出对应边成比例,即可求出结果。
(3)此小题体现“类比”与“转化”思想,将(1)和(2)中的解题方法推广到梯形中求解即可。


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.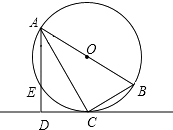
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 ![]() cm,求弦AE的长.
cm,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设篮球、足球、乒乓球、排球四个项目的选修课,为了解同学们的报名情况,随机抽取了部分学生进行调査,将获得的数据进行整理,绘制了如下两幅不完整的统计图,请你根据统计图提供的信息,完成下列问题:

(1)把条形统计图1补充完整,写出图2中C所在扇形的圆心角是 °;
(2)若该校有3000名学生,请你估计全校大约有多少名学生会选修足球课.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简求值
(1)6x+7x2﹣9+4x﹣x2+6
(2)5m﹣2(4m+5n)+3(3m﹣4n)
(3)先化简,再求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣![]() ,b=
,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,点A(﹣4,1)、B(0,1)、C(0,3),
(1)过O的直线l和经过AC的直线平行,求直线l表达式;
(2)已知在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.在直线l上是否存在点P为和谐点?若存在,求出点P坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋子中装有大小完全相同的3粒乒乓球,其中2粒白色,1粒黄色.请你用它为甲、乙两位同学设计一个能决定胜负的公平的摸球游戏规则.并说明公平的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y = ![]() 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.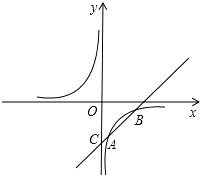
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com