
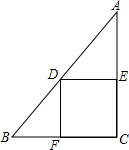
 已知:如图在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF.设DE=x,四边形DECF的面积为y,则y与x之间的函数关系式为y=-2x2+8x.
已知:如图在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF.设DE=x,四边形DECF的面积为y,则y与x之间的函数关系式为y=-2x2+8x. 分析 根据题意求证四边形DECF为矩形,即可推出DF=EC,然后结合图形即可求出AE=8-DF;根据余角的性质即可推出∠A=∠BDF,继而求证△ADE∽△DBF,结合对应边成比例和BF=4-x,AE=8-DF,即可求出DF=-2x+8,根据矩形的面积公式通过等量代换,即可求出二次函数y=DE•DF=-2x2+8x,
解答 解:∵∠C=90°,DE⊥AC,DF⊥BC,
∴四边形DECF为矩形,
∴DF=EC,
∵AC=8,AE=AC-EC,
∴AE=8-DF,
∵∠C=90°,DE⊥AC,DF⊥BC,
∴∠A+∠B=90°,∠BDF+∠ADE=90°,
∴∠A=∠BDF,
∴△ADE∽△DBF,
∴$\frac{AE}{DF}$=$\frac{DE}{BF}$,
∵四边形DECF为矩形,
∴CF=x,CE=DF,
∴BF=BC-CF=4-x,
∵AE=8-DF,
∴$\frac{8-DF}{DF}$=$\frac{x}{4-x}$,
∴DF=-2x+8,
∴y=DE•DF=x(-2x+8)=-2x2+8x.
故答案为:y=-2x2+8x.
点评 本题主要考查相似三角形的判定与性质,勾股定理的应用,矩形的判定与性质,矩形的面积,二次函数的最值等知识点,角的三角函数,关键在于推出AB的长度,求证△ADE∽△DBF,用关于x、y的式子表达出相关的线段,认真的进行计算.


科目:初中数学 来源: 题型:选择题
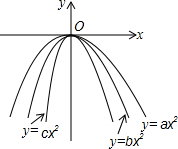 在同一平面直角坐标系内,二次函数y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )
在同一平面直角坐标系内,二次函数y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com