
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻA£½90”ć£¬AB£½4£¬AC£½3£¬MŹĒABÉĻµÄ¶Æµć£Ø²»ÓėA£¬BÖŲŗĻ£©£¬¹żMµć×÷MN”ĪBC½»ACÓŚµćN£®ŅŌMNĪŖÖ±¾¶×÷”ŃO£¬²¢ŌŚ”ŃOÄŚ×÷ÄŚ½Ó¾ŲŠĪAMPN£®ĮīAM£½x£®

£Ø1£©ČēĶ¼1”¢ÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾”÷£ĶNPµÄĆ껿S£»
£Ø2£©ČēĶ¼2”¢”ŃOÓėÖ±ĻßBCĻąĒŠDµć£¬ĒóxµÄÖµĪŖ¶ąÉŁ£æ
£Ø3£©ŌŚ¶ÆµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬¼Ē”÷£ĶNPÓėĢŻŠĪBCNMÖŲŗĻµÄĆ껿ĪŖy£¬ŹŌĒóy¹ŲÓŚxµÄŗÆŹż±ķ“ļŹ½£¬²¢ĒóxĪŖŗĪÖµŹ±£¬yµÄÖµ×ī“ó£¬×ī“óÖµŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©s=![]() £Ø0£¼x£¼4£©£»£Ø2£©x=
£Ø0£¼x£¼4£©£»£Ø2£©x=![]() £»£Ø3£©µ±x=
£»£Ø3£©µ±x=![]() Ź±,yÖµ×ī“ó£¬×ī“óÖµŹĒ2£®
Ź±,yÖµ×ī“ó£¬×ī“óÖµŹĒ2£®
”¾½āĪö”æ
£Ø1£©ÓÉĘ½ŠŠŅ׵Ɣ÷AMN”×”÷ABC£¬øł¾ŻĻąĖĘČż½ĒŠĪ¶ŌÓ¦Ļ߶Ī³É±ČĄżæÉÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾³öAN£¬MN£¬½įŗĻ¾ŲŠĪµÄŠŌÖŹæÉĒó³ö”÷MNPµÄĆ껿£»
£Ø2£©Į¬½ÓOD£¬¹żMµć×÷MQ”ĶBC£¬ÓÉĮ½×é¶ŌÓ¦½Ē·Ö±šĻąµČµÄĮ½øöČż½ĒŠĪĻąĖĘæɵƔ÷BQM”×”÷BAC£¬ÓÉĻąĖĘČż½ĒŠĪ¶ŌÓ¦Ļ߶Ī³É±ČĄżæɵĆxµÄÖµ£»
£Ø3£©MµćŌŚŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬PµćĀäŌŚBCÉĻ£¬Į¬½ÓAP£¬Oµć¾ĶŹĒAPµÄÖŠµć£¬ÓÉ”÷AMO”×”÷ABPĻąĖʵĊŌÖŹæɵĆAM=2£¬·ÖĮ½ÖÖĒéæöĢÖĀŪ¢Łµ±0£¼x”Ü2Ź±£¬ÖŲŗĻ²æ·ÖµÄĆ껿¼“ĪŖ”÷MNPµÄĆ껿£¬ÓÉ£Ø1£©æɵĆy¹ŲÓŚxµÄŗÆŹż±ķ“ļŹ½£¬øł¾ŻxµÄȔֵ·¶Ī§Č·¶Øy×ī“óÖµ¼“æÉ£»¢Śµ±2£¼x£¼4Ź±£¬ÉčPM½»BCÓŚE£¬PN½»BCÓŚF£¬ĄūÓĆ¾ŲŠĪAMPNŗĶĘ½ŠŠĖıߊĪMBFNµÄŠŌÖŹæÉÓĆŗ¬xµÄŹ½×Ó±ķŹ¾³öPF£¬ÓÉ”÷PEF”×”÷ABCµÄŠŌÖŹæɵĆ![]() µÄĆ껿£¬øł¾ŻÖŲŗĻ²æ·ÖµÄĆ껿
µÄĆ껿£¬øł¾ŻÖŲŗĻ²æ·ÖµÄĆ껿![]() æɵĆy¹ŲÓŚxµÄŗÆŹż±ķ“ļŹ½£¬½įŗĻŗÆŹż±ķ“ļŹ½Óė×Ō±äĮæxµÄȔֵ·¶Ī§æɵĆyµÄ×ī“óÖµ.
æɵĆy¹ŲÓŚxµÄŗÆŹż±ķ“ļŹ½£¬½įŗĻŗÆŹż±ķ“ļŹ½Óė×Ō±äĮæxµÄȔֵ·¶Ī§æɵĆyµÄ×ī“óÖµ.
£Ø1£©ŌŚČż½ĒŠĪABCÖŠ”ĻA=900£¬AB=4£¬AC=3
”ąBC=5
ӧMN//BC
”ą”÷AMN”×”÷ABC
”ą![]()
¼“![]()
”ąAN=![]() £¬MN=
£¬MN=![]()
ÓÖ”ßAMPNĪŖ¾ŲŠĪ
ĖłŅŌPM=AN=![]() £¬PN=AM=x
£¬PN=AM=x
ĖłŅŌ”÷MNPµÄĆ껿s=PM”ĮPN”Į![]() =
=![]()
¼“s=![]() £Ø0£¼x£¼4£©
£Ø0£¼x£¼4£©
£Ø2£©AM=x,ŌņMB=4-x
ČēĶ¼£¬Į¬½ÓOD£¬DĪŖĒŠµć£¬¹żMµć×÷MQ”ĶBC£¬QĪŖ“¹×ć£»
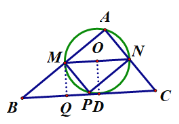
ŅĄĢāŅāæÉµĆ£ŗOD=OM=ON=![]()
”ßMN”ĪBC
”ąOD”ĶBC£¬MQ”ĶBC
”ąMQ=OD=![]()
”ß”ĻA=”ĻMQB=900£¬”ĻB=”ĻB
”ą”÷BQM”×”÷BAC
”ą![]()
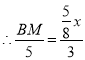
”ąBM=![]()
![]()
”ąx=![]()
ĖłŅŌµ±x=![]() Ź±£¬”ŃOÓėÖ±ĻßBCĻąĒŠDµć.
Ź±£¬”ŃOÓėÖ±ĻßBCĻąĒŠDµć.
£Ø3£©MµćŌŚŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬PµćĀäŌŚBCÉĻ£¬ČēĶ¼

Į¬½ÓAP£¬Oµć¾ĶŹĒAPµÄÖŠµć.
”ßMN”ĪBC
”ą”÷AMO”×”÷ABP
”ą![]()
”ąAM=2
¹Ź·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ
¢Łµ±0£¼x”Ü2Ź±
”÷MNPÓėĢŻŠĪBCNMÖŲŗĻµÄĆ껿![]()
![]()
µ±x=2Ź±£¬yÓŠ×ī“óÖµy=![]()
¢Śµ±2£¼x£¼4Ź±£¬ČēĶ¼
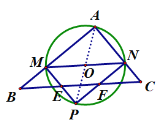
ÉčPM½»BCÓŚE£¬PN½»BCÓŚF
AM=x£¬ŌņMB=4-x
”ßĖıߊĪAMPNŹĒ¾ŲŠĪ£¬
”ąPN”ĪAM£¬PN=AM=x
ÓÖ”ßMN”ĪBC
”ąĖıߊĪMBFNŹĒĘ½ŠŠĖıߊĪ
![]()
![]()
Ó֔ߔ÷PEF”×”÷ABC
”ą![]()
S”÷PEF=![]()
![]()
![]()
![]() =
=![]()
”ąµ±x=![]() Ź±£¬Āś×ć2£¼x£¼4£¬yÓŠ×ī“óÖµ£¬y=2
Ź±£¬Āś×ć2£¼x£¼4£¬yÓŠ×ī“óÖµ£¬y=2
×ŪÉĻĖłŹö£¬µ±x=![]() £¬yÖµ×ī“ó£¬×ī“óÖµŹĒ2£®
£¬yÖµ×ī“ó£¬×ī“óÖµŹĒ2£®


 »īĮ¦ŹŌ¾ķĻµĮŠ“š°ø
»īĮ¦ŹŌ¾ķĻµĮŠ“š°ø æĪæĪÓÅÄÜĮ¦ÅąÓÅ100·ÖĻµĮŠ“š°ø
æĪæĪÓÅÄÜĮ¦ÅąÓÅ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
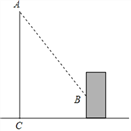
”¾ĢāÄæ”抔×óĶ¬Ń§ĻėĄūÓĆÓ°³¤²āĮæѧŠ£ĘģøĖµÄøß¶Č£¬ČēĶ¼£¬ĖżŌŚÄ³Ņ»Ź±æĢĮ¢Ņ»³¤¶ČĪŖ1Ć׵ıźøĖ£¬²āµĆĘäÓ°³¤ĪŖ![]() Ć×£¬Ķ¬Ź±ĘģøĖĶ¶Ó°µÄŅ»²æ·ÖŌŚµŲÉĻ£¬ĮķŅ»²æ·ÖŌŚÄ³Ņ»½ØÖžĪļµÄĒ½ÉĻ£¬²āµĆĘģøĖÓė½ØÖžĪļµÄ¾ąĄėĪŖ10Ć×£¬ĘģøĖŌŚĒ½ÉĻµÄÓ°øßĪŖ2Ć×£¬Ēė°ļŠ”×óĶ¬Ń§Ėć³öѧŠ£ĘģøĖµÄøß¶Č£®
Ć×£¬Ķ¬Ź±ĘģøĖĶ¶Ó°µÄŅ»²æ·ÖŌŚµŲÉĻ£¬ĮķŅ»²æ·ÖŌŚÄ³Ņ»½ØÖžĪļµÄĒ½ÉĻ£¬²āµĆĘģøĖÓė½ØÖžĪļµÄ¾ąĄėĪŖ10Ć×£¬ĘģøĖŌŚĒ½ÉĻµÄÓ°øßĪŖ2Ć×£¬Ēė°ļŠ”×óĶ¬Ń§Ėć³öѧŠ£ĘģøĖµÄøß¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
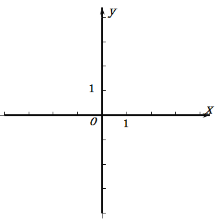
”¾ĢāÄæ”æŅŃÖŖĘ½ĆęÖ±½Ē×ų±źĻµxOy£ØČēĶ¼1£©£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼ĻńÓėyÖį½»ÓŚµćA£¬µćMŌŚÕż±ČĄżŗÆŹż
µÄĶ¼ĻńÓėyÖį½»ÓŚµćA£¬µćMŌŚÕż±ČĄżŗÆŹż![]() µÄĶ¼ĻńÉĻ£¬ĒŅMO£½MA£®¶ž“ĪŗÆŹży£½x2£«bx£«cµÄĶ¼Ļń¾¹żµćA”¢M£®
µÄĶ¼ĻńÉĻ£¬ĒŅMO£½MA£®¶ž“ĪŗÆŹży£½x2£«bx£«cµÄĶ¼Ļń¾¹żµćA”¢M£®
£Ø1£©ĒóĻ߶ĪAMµÄ³¤£»
£Ø2£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø3£©Čē¹ūµćBŌŚyÖįÉĻ£¬ĒŅĪ»ÓŚµćAĻĀ·½£¬µćCŌŚÉĻŹö¶ž“ĪŗÆŹżµÄĶ¼ĻńÉĻ£¬µćDŌŚŅ»“ĪŗÆŹż![]() µÄĶ¼ĻńÉĻ£¬ĒŅĖıߊĪABCDŹĒĮāŠĪ£¬ĒóµćCµÄ×ų±ź£®
µÄĶ¼ĻńÉĻ£¬ĒŅĖıߊĪABCDŹĒĮāŠĪ£¬ĒóµćCµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóÓėxÖį½»ÓŚµćA£Ø©1£¬0£©£¬ÓėyÖįµÄ½»µćBŌŚ£Ø0£¬©2£©ŗĶ£Ø0£¬©1£©Ö®¼ä£Ø²»°üĄØÕāĮ½µć£©£¬¶Ō³ĘÖįĪŖÖ±Ļßx=1£®ĻĀĮŠ½įĀŪ£ŗ¢Łabc£¾0 ¢Ś4a+2b+c£¾0 ¢Ū4ac©b2£¼8a ¢Ü![]() £¼a£¼
£¼a£¼![]() ¢Żb£¾c£®ĘäÖŠŗ¬ĖłÓŠÕżČ·½įĀŪµÄŃ”ĻīŹĒ£Ø””””£©
¢Żb£¾c£®ĘäÖŠŗ¬ĖłÓŠÕżČ·½įĀŪµÄŃ”ĻīŹĒ£Ø””””£©

A. ¢Ł¢Ū B. ¢Ł¢Ū¢Ü C. ¢Ś¢Ü¢Ż D. ¢Ł¢Ū¢Ü¢Ż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() ”¢
”¢![]() Į½µć£¬Óė
Į½µć£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() ,Å×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļß
,Å×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļß![]() £¬½»Å×ĪļĻßÓŚµć
£¬½»Å×ĪļĻßÓŚµć![]() ,½»
,½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £®
£®
 ””””””””
”””””””” ””””””””
””””””””
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½¼°µć![]() ”¢µć
”¢µć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø2£©Å×ĪļĻ߶Ō³ĘÖįÉĻµÄŅ»¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÉĻŌĖ¶Æ£¬Į¬½Ó
³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÉĻŌĖ¶Æ£¬Į¬½Ó![]() £¬
£¬![]() £¬ÉčŌĖ¶ÆŹ±¼äĪŖ
£¬ÉčŌĖ¶ÆŹ±¼äĪŖ![]() Ćė£Ø
Ćė£Ø![]() £©£¬ŌŚµć
£©£¬ŌŚµć![]() µÄŌĖ¶Æ¹ż³ĢÖŠ£¬ĒėĒó³ö£ŗµ±
µÄŌĖ¶Æ¹ż³ĢÖŠ£¬ĒėĒó³ö£ŗµ±![]() ĪŖŗĪÖµŹ±£¬
ĪŖŗĪÖµŹ±£¬![]() £æ
£æ
£Ø3£©Čōµć![]() ŌŚÅ×ĪļĻßÉĻ
ŌŚÅ×ĪļĻßÉĻ![]() ”¢
”¢![]() Į½µćÖ®¼äŌĖ¶Æ£Øµć
Į½µćÖ®¼äŌĖ¶Æ£Øµć![]() ²»Óėµć
²»Óėµć![]() ”¢
”¢![]() ÖŲŗĻ£©£¬ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬Éčµć
ÖŲŗĻ£©£¬ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬
£¬![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó
µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó![]() ĪŖŗĪÖµŹ±
ĪŖŗĪÖµŹ±![]() ÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ¶ąÉŁ£æ
ÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻÓėĢ½¾æ£ŗ
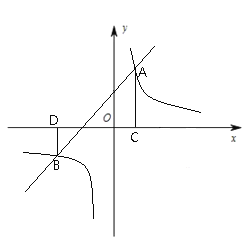
ČēĶ¼ĖłŹ¾£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß![]() Óė·“±ČĄżŗÆŹż
Óė·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó½»ÓŚ
µÄĶ¼Ļó½»ÓŚ![]() £¬
£¬![]() Į½µć£¬¹żµć
Į½µć£¬¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() £®
£®
£Ø1£©Ēó![]() £¬
£¬![]() µÄÖµ¼°·“±ČĄżŗÆŹżµÄŗÆŹż±ķ“ļŹ½£»
µÄÖµ¼°·“±ČĄżŗÆŹżµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©Čōµć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() £¬ĒėĒó³ö“ĖŹ±µć
£¬ĒėĒó³ö“ĖŹ±µć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø3£©Š”Ó±ŌŚĢ½Ė÷ÖŠ·¢ĻÖ£ŗŌŚ![]() ÖįÕż°ėÖįÉĻ“ęŌŚµć
ÖįÕż°ėÖįÉĻ“ęŌŚµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖ¶„½ĒµÄµČŃüČż½ĒŠĪ.ĒėÄćÖ±½ÓŠ“³öµć
ĪŖ¶„½ĒµÄµČŃüČż½ĒŠĪ.ĒėÄćÖ±½ÓŠ“³öµć![]() µÄ×ų±ź.
µÄ×ų±ź.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
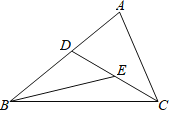
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬DĪŖ±ßABÉĻŅ»µć£¬EŹĒCDµÄÖŠµć£¬ĒŅ”ĻACD£½”ĻABE£®ŅŃÖŖAC£½2£¬ÉčAB£½x£¬AD£½y£¬ŌņyÓėxĀś×ćµÄ¹ŲĻµŹ½ĪŖ£Ø””””£©
A.xy£½4B.2xy©y2£½4C.xy©y2£½4D.x2+xy©2y2£½4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
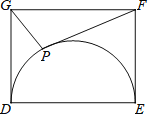
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬ČōOĪŖBC±ßµÄÖŠµć£¬Ōņ±ŲÓŠ£ŗAB2+AC2=2AO2+2BO2³ÉĮ¢£®ŅĄ¾ŻŅŌÉĻ½įĀŪ£¬½ā¾öČēĻĀĪŹĢā£ŗČēĶ¼£¬ŌŚ¾ŲŠĪDEFGÖŠ£¬ŅŃÖŖDE=4£¬EF=3£¬µćPŌŚŅŌDEĪŖÖ±¾¶µÄ°ėŌ²ÉĻŌĖ¶Æ£¬ŌņPF2+PG2µÄ×īŠ”ÖµĪŖ£Ø””””£©
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»øö²»ĶøĆ÷µÄŠ”²¼“ü֊װӊ4øöÖŹµŲ”¢“óŠ”ĶźČ«ĻąĶ¬µÄŠ”Ēņ£¬ĖüĆĒ·Ö±š±źÓŠŹż×Ö0£¬1£¬2£¬3£¬Š”Ć÷“Ó²¼“üĄļĖ껜ƞ³öŅ»øöŠ”Ēņ£¬¼ĒĻĀŹż×ÖĪŖ![]() £¬Š”ŗģŌŚŹ£ĻĀµÄ3øöŠ”ĒņÖŠĖ껜ƞ³öŅ»øöŠ”Ēņ£¬¼ĒĻĀŹż×ÖĪŖ
£¬Š”ŗģŌŚŹ£ĻĀµÄ3øöŠ”ĒņÖŠĖ껜ƞ³öŅ»øöŠ”Ēņ£¬¼ĒĻĀŹż×ÖĪŖ![]() £¬Õāѳȷ¶ØĮĖµć
£¬Õāѳȷ¶ØĮĖµć![]() µÄ×ų±ź
µÄ×ų±ź![]() £®
£®
£Ø1£©»Ź÷דĶ¼»ņĮŠ±ķ£¬Š“³öµć![]() ĖłÓŠæÉÄܵÄ×ų±ź£»
ĖłÓŠæÉÄܵÄ×ų±ź£»
£Ø2£©Š”Ć÷ŗĶŠ”ŗģŌ¼¶Ø×öŅ»øöÓĪĻ·£¬Ęä¹ęŌņĪŖ£ŗČō![]() ŌŚµŚŅ»ĻóĻŽ£¬ŌņŠ”Ć÷Ź¤£»·ńŌņ£¬Š”ŗģŹ¤£»ÕāøöÓĪĻ·¹«Ę½Āš£æĒėÄć×÷³öÅŠ¶Ļ²¢ĖµĆ÷ĄķÓÉ£®
ŌŚµŚŅ»ĻóĻŽ£¬ŌņŠ”Ć÷Ź¤£»·ńŌņ£¬Š”ŗģŹ¤£»ÕāøöÓĪĻ·¹«Ę½Āš£æĒėÄć×÷³öÅŠ¶Ļ²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com