
【题目】如图1所示,已知函数y= (x>0)图像上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0) .动点M是y轴正半轴上点B上方的点.动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q.连接AQ,取AQ的中点C.
(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时, 若四边形BQNC是菱形,面积为2,求此时P点的坐标.
(3)在(2)的条件下,在平面直角坐标系中是否存在点S,使得以点D、Q、N、S为顶点的四边形为平行四边
形,如果存在,请直接写出所有的点S的坐标;如果不存在,请说明理由.

【答案】(1)、3;(2)、(3,2);(3)、(1,4![]() ),(1,0),(5,4
),(1,0),(5,4![]() )
)
【解析】试题分析:(1)、连接OP,根据三角形的面积计算法则进行求解;(2)、根据四边形BQNC是菱形得出BQ=BC=NQ,∠BQC=∠NQC,根据AB⊥BQ,C是AQ的中点,得出BC=CQ=![]() AQ,∠BQC=60°,∠BAQ=30°,从而说明△ABQ和△ANQ全等,得出∠BAQ=∠NAQ=30°,∠BAO=30°,设CQ=BQ=x,根据菱形的面积求出x的值,即BQ的长度,根据Rt△AQB的勾股定理求出OA的长度,根据反比例函数的性质得出点P的坐标.
AQ,∠BQC=60°,∠BAQ=30°,从而说明△ABQ和△ANQ全等,得出∠BAQ=∠NAQ=30°,∠BAO=30°,设CQ=BQ=x,根据菱形的面积求出x的值,即BQ的长度,根据Rt△AQB的勾股定理求出OA的长度,根据反比例函数的性质得出点P的坐标.
试题解析:(1)、连接OP,S△PAB=S△PAO=![]() xy=
xy=![]() ×6=3
×6=3
(2)、∵四边形BQNC是菱形,∴BQ=BC=NQ,∠BQC=∠NQC
∵AB⊥BQ,C是AQ的中点,∴BC=CQ=![]() AQ,∴∠BQC=60°,∠BAQ=30°
AQ,∴∠BQC=60°,∠BAQ=30°
在△ABQ和△ANQ中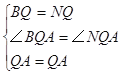 ∴△ABQ≌△ANQ ,∴∠BAQ=∠NAQ=30°,∴∠BAO=30°
∴△ABQ≌△ANQ ,∴∠BAQ=∠NAQ=30°,∴∠BAO=30°
∵S菱形BQNC=![]() =
=![]() ×CQ×BN,设CQ=BQ=x,则BN=2×(x×
×CQ×BN,设CQ=BQ=x,则BN=2×(x×![]() )=
)=![]() x,∴x=2,∴BQ=2
x,∴x=2,∴BQ=2
∵在Rt△AQB中,∠BAQ=30°,∴AB=![]() BQ=2
BQ=2![]() ,∵∠BAO=30°∴OA=
,∵∠BAO=30°∴OA=![]() AB=3,
AB=3,
又∵P点在函数y=![]() 的图象上,∴P点坐标为(3,2);
的图象上,∴P点坐标为(3,2);
(3)、![]() ·
·


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].

(1)、如图①,对△ABC作变换[50°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)、如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)、如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)、求证:DE⊥AG;
(2)、如图2,正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°),得到正方形OE′F′G′;
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为2,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
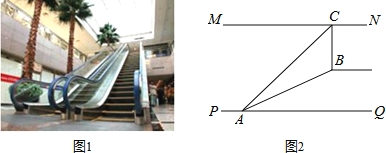
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜兴紧靠太湖,所产百合有“太湖人参”之美誉,今年百合上市后,甲、乙两超市分别用12000元以相同的进价购进质量相同的百合,甲超市销售方案是:将百合按分类包装销售,其中挑出优质的百合400千克,以进价的2倍价格销售,剩下的百合以高于进价10%销售.乙超市的销售方案是:不将百合分类,直接包装销售,价格按甲超市分类销售的两种百合单价和的一半定价.若两超市将百合全部售完,其中甲超市获利8400元(其它成本不计).问:
(1)百合进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线的形状与y=﹣2x2+2的形状相同,且顶点坐标是(4,﹣2),则它的解析式是( )
A.y=2(x﹣4)2﹣2
B.y=﹣2(x﹣4)2﹣2
C.y=﹣2(x﹣4)2+2
D.y=﹣2(x+4)2﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com