
【题目】如图,在直角坐标系中, ![]() 的直角边AC在x轴上,
的直角边AC在x轴上, ![]() ,反比例函数
,反比例函数![]() 的图象经过BC边的中点
的图象经过BC边的中点![]() .
.
![]() 求这个反比例函数的表达式;
求这个反比例函数的表达式;
![]() 若
若![]() 与
与![]() 成中心对称,且
成中心对称,且![]() 的边FG在y轴的正半轴上,点E在这个函数的图象上.
的边FG在y轴的正半轴上,点E在这个函数的图象上.
![]() 求OF的长;
求OF的长;
![]() 连接
连接![]() ,证明四边形ABEF是正方形.
,证明四边形ABEF是正方形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学校准备用9万元购进50台电视机,为了节省费用,学校打算以出厂价从厂家直接采购,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若学校同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下学校的采购方案;
(2)若学校去商场购买,在出厂价相同的情况下,商场销售一台甲种电视机获利150元,销售一台乙种电视机获利200元,销售一台丙种电视机获利250元,在(1)的条件下,学校选择哪种方案省下的钱最多?
(3)若学校准备用9万元同时购进三种不同的电视机50台,请你设计进货方案(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民营企业准备用14000元从外地购进A、B两种商品共600件,其中A种商品的成本价为20元,B种商品的成本价为30元.
(1)该民营企业从外地购得A、B两种商品各多少件?
(2)该民营企业计划租用甲、乙两种货车共6辆,一次性将A、B两种商品运往某城市,已知每辆甲种货车最多可装A种商品110件和B种商品20件;每辆乙种货车最多可装A种商品30件和B种商品90件,问安排甲、乙两种货车有几种方案?请你设计出具体的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:当(x﹣2)2+|y+1|=0时,求代数式4(![]() x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值;
x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值;
(2)关于x的代数式(x2+2x)﹣[kx2﹣(3x2﹣2x+1)]的值与x无关,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知∠AOB=25°42′,则∠AOB的余角为 ,∠AOB的补角为 ;
(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代数式表示∠MON的大小;
(3)如图,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,且∠AOB=25°,则经过多少时间后,△AOB的面积第一次达到最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2) ![]()
(3)﹣2.5÷![]() ×(﹣
×(﹣![]() )
)
(4)![]() ÷(﹣2
÷(﹣2![]() )﹣
)﹣![]() ×
×![]() ﹣
﹣![]() ÷4
÷4
(5)![]()
(6)(﹣2)2×5﹣(﹣2)3÷4
(7)![]() ;
;
(8)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
(1)本次被调查的学员共有 人;在被调查者中参加“科目3”测试的有 人;将条形统计图补充完整;
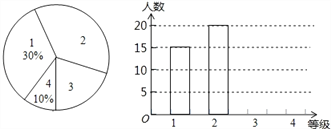
(2)该考点参加“科目4”考试的学员里有3位是教师,某新闻部门准备在该考点参加“科目4”考试的学员中随机选出2位,调查他们对新规的了解情况,请你用列表法或画树状图的方法求出所选两位学员恰好都是教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1) (﹣8) +3=__ (2) ﹣3﹣6= __ (3) ﹣3×2= __ (4) ﹣9÷(﹣3) =__
(5) 0×(﹣2019) =__ (6) ![]() (7) (2)2×32= (8) (2)3÷(﹣1)5 =
(7) (2)2×32= (8) (2)3÷(﹣1)5 =
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 和点和
和点和![]() .
.
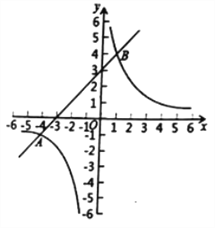
(1)求这两个函数的表达式;
(2)观察图象,当![]() 时,直接写出自变量
时,直接写出自变量![]() 的取值范围;
的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com