
ЁОЬтФПЁПШчЭМ1ЃЌвЛУЖжЪЕиОљдШЕФїЛзгЃЌїЛзггаСљИіУцВЂЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6.ШчЭМ2ЃЌга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() 7ИіШІЃЌЯрСкСНИіШІМфОрЯрЕШ.ЬјШІгЮЯЗЕФЙцдђЮЊЃКгЮЯЗепУПжРвЛДЮїЛзгЃЌїЛзгЯђЩЯЕФвЛУцЩЯЕФЪ§зжЪЧМИЃЌОЭДгШІ
7ИіШІЃЌЯрСкСНИіШІМфОрЯрЕШ.ЬјШІгЮЯЗЕФЙцдђЮЊЃКгЮЯЗепУПжРвЛДЮїЛзгЃЌїЛзгЯђЩЯЕФвЛУцЩЯЕФЪ§зжЪЧМИЃЌОЭДгШІ![]() ПЊЪМЯђЧАСЌајЬјМИИіМфОр.ШчЃКДгШІ
ПЊЪМЯђЧАСЌајЬјМИИіМфОр.ШчЃКДгШІ![]() Ц№ЬјЃЌЕквЛДЮжРЕУ3ЃЌОЭСЌајЬј3ИіМфОрЃЌЬјЕНШІ
Ц№ЬјЃЌЕквЛДЮжРЕУ3ЃЌОЭСЌајЬј3ИіМфОрЃЌЬјЕНШІ![]() ЃЛШєЕкЖўДЮжРЕУ3ЃЌОЭДг
ЃЛШєЕкЖўДЮжРЕУ3ЃЌОЭДг![]() ПЊЪМСЌајЬј3ИіМфОрЃЌЬјЕНШІ
ПЊЪМСЌајЬј3ИіМфОрЃЌЬјЕНШІ![]() ЃЛШєЕкЖўДЮжРЕУ4ЃЌОЭДгШІ
ЃЛШєЕкЖўДЮжРЕУ4ЃЌОЭДгШІ![]() ПЊЪМСЌајЬј4ИіМфОрЃЌЬјЕНШІ
ПЊЪМСЌајЬј4ИіМфОрЃЌЬјЕНШІ![]() КѓЗЕЛиЕНШІ
КѓЗЕЛиЕНШІ![]() ЃЛЁЩшгЮЯЗепДгШІ
ЃЛЁЩшгЮЯЗепДгШІ![]() Ц№Ьј.
Ц№Ьј.
ЃЈ1ЃЉаЁУїЫцЛњжРвЛДЮїЛзгЃЌЧѓЬјЕНШІ![]() ЕФИХТЪ
ЕФИХТЪ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉаЁССЫцЛњжРСНДЮїЛзгЃЌгУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓзюКѓЬјЕНШІ![]() ЕФИХТЪ
ЕФИХТЪ![]() ЃЌВЂжИГіЫћгыаЁУїЬјЕНШІ
ЃЌВЂжИГіЫћгыаЁУїЬјЕНШІ![]() ЕФПЩФмадвЛбљТ№ЃП
ЕФПЩФмадвЛбљТ№ЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() .ЃЈ2ЃЉаЁССгыаЁУїЬјЕНШІ
.ЃЈ2ЃЉаЁССгыаЁУїЬјЕНШІ![]() ЕФПЩФмадВЛвЛбљ.
ЕФПЩФмадВЛвЛбљ.
ЁОНтЮіЁП
(1) вЛИіїЛзгга6ИіУцЃЌЫљвдЙВга6жжЕШПЩФмЕФНсЙћЃЌЬјЕНШІ![]() ЕФжЛга1жжЧщПіЃЌЫљвдаЁУїЬјЕНШІ
ЕФжЛга1жжЧщПіЃЌЫљвдаЁУїЬјЕНШІ![]() ЕФИХТЪ
ЕФИХТЪ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЭЈЙ§СаБэПЩЕУЙВга36жжПЩФмЕФНсЙћЃЌзюКѓЬјЕНШІ![]() га
га![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВЮхжжЧщПі. ЫљвдзюКѓаЁССЬјЕНШІ
ЙВЮхжжЧщПі. ЫљвдзюКѓаЁССЬјЕНШІ![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]() ЃЌМДаЁССгыаЁУїЬјЕНШІ
ЃЌМДаЁССгыаЁУїЬјЕНШІ![]() ЕФПЩФмадВЛвЛбљ.
ЕФПЩФмадВЛвЛбљ.
НтЃКЃЈ1ЃЉЁпаЁУїЫцЛњжРвЛДЮїЛзгЃЌЙВга6жжЕШПЩФмЕФНсЙћЃЌЬјЕНШІ![]() ЕФжЛга1жжЧщПіЃЌ
ЕФжЛга1жжЧщПіЃЌ
МДїЛзгжРЕН6ЪБЃЌ
ЁрЬјЕНШІ![]() ЕФИХТЪ
ЕФИХТЪ![]() .
.
ЃЈ2ЃЉСаБэЗЈЃК
ЕквЛДЮ ЕкЖўДЮ | 1 | 2 | 3 | 4 | 5 | 6 |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
ЁпЙВга36жжЕШПЩФмЕФНсЙћЃЌзюКѓЬјЕНШІ![]() га
га![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВЮхжжЧщПі.
ЙВЮхжжЧщПі.
ЁрзюКѓЬјЕНШІ![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]() .
.
ЁраЁССгыаЁУїЬјЕНШІ![]() ЕФПЩФмадВЛвЛбљ.
ЕФПЩФмадВЛвЛбљ.


 ПМЧАБиСЗЯЕСаД№АИ
ПМЧАБиСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйХзЮяЯпyЃНax2+bx+3ЃЈaЁй0ЃЉгыxжсЃЌyжсЗжБ№НЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЕуCШ§ЕуЃЎ
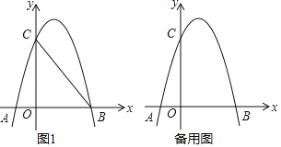
ЃЈ1ЃЉЪдЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDЃЈ2ЃЌmЃЉдкЕквЛЯѓЯоЕФХзЮяЯпЩЯЃЌСЌНгBCЃЌBDЃЎЪдЮЪЃЌдкЖдГЦжсзѓВрЕФХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌТњзуЁЯPBCЃНЁЯDBCЃПШчЙћДцдкЃЌЧыЧѓГіЕуPЕуЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуNдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЕуMдкХзЮяЯпЩЯЃЌЕБвдMЁЂNЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЮхвЛЁБЧАЯІЃЌФГОЯњЩЬМЦЛЎЛЈ23500дЊЙКТђAЁЂBЁЂCШ§жжаТПюЪБзАЙВ50ЬзНјааЪдЯњЃЌВЂЧвЙКНјЕФCжжЪБзАЬзЪ§ВЛЩйгкBжжЪБзАЬзЪ§ЃЌЧвВЛГЌЙ§AжжЪБзАЬзЪ§ЃЌЩшЙКНјAжжЪБзАxЬзЃЌBжжЪБзАyЬзЃЌШ§жжЪБзАЕФНјМлКЭЪлМлШчЯТБэЫљЪОЃЎ
аЭКХ | A | B | C |
НјМлЃЈдЊ/ЬзЃЉ | 400 | 550 | 500 |
ЪлМлЃЈдЊ/ЬзЃЉ | 500 | 700 | 650 |
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉТњзуЬѕМўЕФНјЛѕЗНАИгаФФМИжжЃПаДГіНтД№Й§ГЬЃЛ
ЃЈ3ЃЉМйЩшЫљЙКНјЕФетШ§жжЪБзАФмШЋВПТєГіЃЌЧвдкЙКЯњетХњЪБзАЕФЙ§ГЬжаашвЊСэЭтжЇГіИїжжЗбгУ1000дЊЃЎЭЈЙ§МЦЫуХаЖЯФФжжНјЛѕЗНАИРћШѓзюДѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2011ЩНЖЋМУФЯЃЌ27ЃЌ9ЗжЃЉШчЭМЃЌОиаЮOABCжаЃЌЕуOЮЊдЕуЃЌЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎХзЮяЯп![]() ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮBCЩЯвЛИіЖЏЕуЃЈВЛгыЕуCжиКЯЃЉЃЌЕуQЮЊЯпЖЮACЩЯвЛИіЖЏЕуЃЌAQ=CPЃЌСЌНгPQЃЌЩшCP=mЃЌЁїCPQЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкmЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіmЮЊКЮжЕЪБЃЌSШЁЕУзюДѓжЕЃЛ
ЂкЕБSзюДѓЪБЃЌдкХзЮяЯп![]() ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+cЕФЖдГЦжсЮЊxЃНЉ1ЃЌЧвЙ§ЕуЃЈЉ3ЃЌ0ЃЉЃЌЃЈ0ЃЌЉ3ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЎ
ЃЈ2ЃЉвбжЊЕуЃЈmЃЌkЃЉКЭЕуЃЈnЃЌkЃЉдкДЫХзЮяЯпЩЯЃЌЦфжаmЁйnЃЌЧыХаЖЯЙигкtЕФЗНГЬt2+mt+nЃН0ЪЧЗёгаЪЕЪ§ИљЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
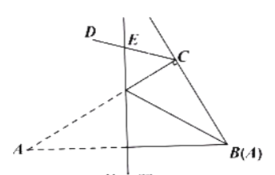
ЁОЬтФПЁПШчЭМЫљЪОЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌелКлЫљдкжБЯпНЛ
ДІЃЌелКлЫљдкжБЯпНЛ![]() ЕФЭтНЧЦНЗжЯп
ЕФЭтНЧЦНЗжЯп![]() гкЕу
гкЕу![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ______ЃЎ
ЕФОрРыЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
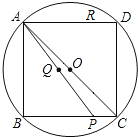
ЁОЬтФПЁПШчЭМЃЌ![]() ФкНггкЁбOЃЌ
ФкНггкЁбOЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЁбOЩЯгыЕу
ЪЧЁбOЩЯгыЕу![]() ЙигкдВаФ
ЙигкдВаФ![]() ГЩжааФЖдГЦЕФЕуЃЌ
ГЩжааФЖдГЦЕФЕуЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯвЛЕуЃЌСЌНс
БпЩЯвЛЕуЃЌСЌНс![]() ЃЎвбжЊ
ЃЎвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌСЌНс
ЩЯвЛЖЏЕуЃЌСЌНс![]() ВЂбгГЄНЛЫФБпаЮ
ВЂбгГЄНЛЫФБпаЮ![]() ЕФвЛБпгкЕу
ЕФвЛБпгкЕу![]() ЃЌЧвТњзу
ЃЌЧвТњзу![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ_______________ЃЎ
ЕФжЕЮЊ_______________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉx+5гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуDЃЌХзЮяЯпyЃНЉx2+bx+cгыжБЯпyЃНЉx+5НЛгкBЃЌDСНЕуЃЌЕуCЪЧХзЮяЯпЕФЖЅЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуMЪЧжБЯпBDЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЦфКсзјБъЮЊmЃЌЙ§ЕуMзїxжсЕФДЙЯпЃЌНЛжБЯпBDгкЕуPЃЌЕБЯпЖЮPMЕФГЄЖШзюДѓЪБЃЌЧѓmЕФжЕМАPMЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдквьгкBЁЂDЕФЕуQЃЌЪЙЁїBDQжаBDБпЩЯЕФИпЮЊ3![]() ЃЌШєДцдкЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЃЌШєДцдкЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП НёФъ5дТЗнЃЌЮвЪаФГжабЇПЊеЙељзіЁАЮхКУаЁЙЋУёЁБеїЮФБШШќЛюЖЏЃЌШќКѓЫцЛњГщШЁСЫВПЗжВЮШќбЇЩњЕФГЩМЈЃЌАДЕУЗжЛЎЗжЮЊAЃЌBЃЌCЃЌDЫФИіЕШМЖЃЌВЂЛцжЦСЫШчЯТВЛЭъећЕФЦЕЪ§ЗжВМБэКЭЩШаЮЭГМЦЭМЃК
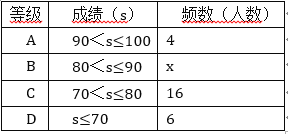
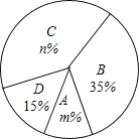
ИљОнвдЩЯаХЯЂЃЌНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉБэжаЕФx=______ЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаm=______ЃЌn=______ЃЌCЕШМЖЖдгІЕФЩШаЮЕФдВаФНЧЮЊ______ЖШЃЛ
ЃЈ3ЃЉИУаЃзМБИДгЩЯЪіЛёЕУAЕШМЖЕФЫФУћбЇЩњжабЁШЁСНШЫзіЮЊбЇаЃЁАЮхКУаЁЙЋУёЁБжОдИепЃЌвбжЊетЫФШЫжагаСНУћФаЩњЃЈгУa1ЃЌa2БэЪОЃЉКЭСНУћХЎЩњЃЈгУb1ЃЌb2БэЪОЃЉЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓЧЁКУбЁШЁЕФЪЧa1КЭb1ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com