练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．规定“*”表示一种运算，且a*b=$\frac{a-2b}{ab}$，试求3*（4*$\frac{1}{2}$）的值．

    分析 原式利用题中的新定义计算即可得到结果．

    解答 解：根据题中的新定义得：3*（4*$\frac{1}{2}$）=3*$\frac{3}{2}$=$\frac{3-3}{3×\frac{3}{2}}$=0．

    点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．若x=a+1是不等式$\frac{1}{2}x$-1＜2的解，则a＜5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．上海世博会区间，某博物馆每周都吸引大量中外游客前来参观，如果游客过多，对馆中的珍贵文物会产生不利影响，但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入．因此，博物馆采取了涨浮门票价格的方法来控制参观人数，在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系，在这样的情况下．
    （1）如果确保每周4万元的门票收入，那么每周应限定参观人数是多少？门票价格应是多少元？
    （2）门片价格应该是多少元时门票收入最大，这样每周应有多少人参观？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

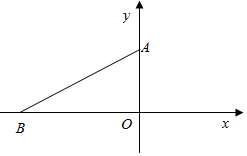    5．如图，已知Rt△OAB，∠OAB=60°，∠AOB=90°，O点与坐标系原点重合，若点P在x轴上，且△APB是等腰三角形，则点P的坐标可能有（　　）个．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知a：b：c=2：3：4，且a-2b+3c=20，则a+2b-3c=-10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列说法正确的是（　　）
    A．如果两个三角形全等，则它们是关于某条直线成轴对称的图形
    B．如果两个三角形关于某条直线成轴对称，那么它们是全等三角形
    C．等边三角形是关于一条边上的中线成轴对称的图形
    D．一条线段是关于经过该线段中点的中线成轴对称的图形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图所示，点P是射线OC上任意一点，PD⊥OA于点D，PE⊥OB于点E，当OC平分∠AOB时，可以得到PD=PE，反过来，当PD=PE时，OC平分∠AOB吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．我市某地的一种水产品由于运输原因，长期只能在当地销售，当地政府对该水产品的销售投资收益为：每投入x万元，可获得利润p=-$\frac{1}{25}$（x-60）2+40（万元），当地政府拟在“十二•五”规划中加快开发该水产品的销售，其规划方案为：
    在规划前后对该项目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出50万元用于修建一条公路，两年修成，通车前该水产品只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售，在外地销售的投资收益为：每投入x万元，可获利润w=-$\frac{24}{25}$（100-x）2+$\frac{276}{5}$（100-x）+160（万元）．
    （1）若不进行开发，求5年所获利润的最大值是多少？
    （2）若按规划实施，求5年所获利润（扣除修路费用）的最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）-9+5×（-6）-12÷（-6）；
    （2）36×（-$\frac{1}{6}$+$\frac{3}{4}$+$\frac{1}{3}$-$\frac{1}{12}$）；
    （3）-12-（1-0.5）×$\frac{1}{3}$×[2-（-3）2]．

    查看答案和解析>>

    同步练习册答案