
【题目】如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
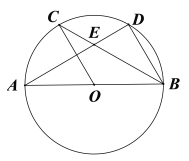
(1)求证:![]() ;
;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
【答案】(1)证明见解析;(2)半径为![]() ;(3)PQ=
;(3)PQ=![]()
【解析】
(1)由等腰三角形的性质和平行线的性质可得∠OBC=∠CBD,即可证![]() ;
;
(2)通过证明△ACE∽△BCA,可得![]() ,可得AC=2,由勾股定理可求AB的长,即可求⊙O的半径;
,可得AC=2,由勾股定理可求AB的长,即可求⊙O的半径;
(3)过点O作OH⊥FQ于点H,连接OQ,通过证明△APC∽△CPB,可得![]() ,可求PA=
,可求PA=![]() ,即可求PO的长,通过证明△PHO∽△BCA,
,即可求PO的长,通过证明△PHO∽△BCA,
可求PH,OH的长,由勾股定理可求HQ的长,即可求PQ的长.
解:(1)∵OC=OB
∴∠OBC=∠OCB
∵OC∥BD
∴∠OCB=∠CBD
∴∠OBC=∠CBD
∴![]()
(2)连接AC,
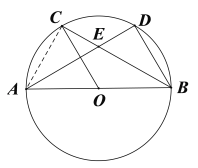
∵CE=1,EB=3,
∴BC=4
∵![]()
∴∠CAD=∠ABC,且∠ACB=∠ACB
∴△ACE∽△BCA
∴![]()
∴AC2=CBCE=4×1
∴AC=2,
∵AB是直径
∴∠ACB=90°
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.
(3)如图,过点O作OH⊥FQ于点H,连接OQ,

∵PC是⊙O切线,
∴∠PCO=90°,且∠ACB=90°
∴∠PCA=∠BCO=∠CBO,且∠CPB=∠CPA
∴△APC∽△CPB
∴![]() ,
,
∴PC=2PA,PC2=PAPB
∴4PA2=PA×(PA+2![]() )
)
∴PA=![]() ,
,
∴PO=![]() ,
,
∵PQ∥BC
∴∠CBA=∠BPQ,且∠PHO=∠ACB=90°
∴△PHO∽△BCA
∴![]() ,
,
即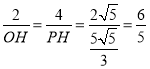 ,
,
∴PH=![]() ,OH=
,OH=![]() ,
,
∴HQ=![]() ,
,
∴PQ=PH+HQ=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了解某灯管的使用寿命,可以采用普查的方式进行
C.甲乙两组身高数据的方差分别为![]() 、
、![]() ,那么乙组的身高比较整齐
,那么乙组的身高比较整齐
D.一组数据3,5,4,5,6,7的众数、中位数和平均数都是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年疫情期间,长沙市教育局出台《长沙市中小学线上教学工作实施意见》,长沙市推出名师公益大课堂,为学生提供线上直播教学,据统计,第一批公益课受益学生
年疫情期间,长沙市教育局出台《长沙市中小学线上教学工作实施意见》,长沙市推出名师公益大课堂,为学生提供线上直播教学,据统计,第一批公益课受益学生![]() 万人次,第三批公益课受益学生
万人次,第三批公益课受益学生![]() 万人次.
万人次.
(1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E,CF∥AB交AD延长线于点F,连接BF交⊙O于点G,连接DG.
(1)求证:DE为⊙O的切线;
(2)求证:四边形ABFC为菱形;
(3)若OA=5,DG=2![]() ,求线段GF的长.
,求线段GF的长.
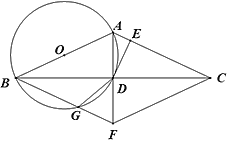
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形 ABCD的两条对角线相交于点O, E是BO的中点.过B点作AC的平行线,交CE的延长线于点F,连接BF.
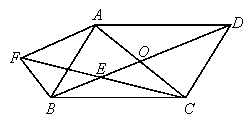
(1)求证:FB=AO;
(2)当平行四边形 ABCD满足什么条件时,四边形AFBO是菱形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 城出发匀速行驶至
城出发匀速行驶至![]() 城.在整个行驶过程中,甲、乙两车离
城.在整个行驶过程中,甲、乙两车离![]() 城的距离
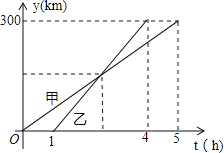
城的距离![]() (千米)与甲车行驶的时间
(千米)与甲车行驶的时间![]() (小时)之间的函数关系如图所示.则下列结论:
(小时)之间的函数关系如图所示.则下列结论:
①![]() 两城相距
两城相距![]() 千米;
千米;
②乙车比甲车晚出发![]() 小时,却早到
小时,却早到![]() 小时;
小时;
③乙车出发后![]() 小时追上甲车;
小时追上甲车;
④当甲、乙两车相距![]() 千米时,
千米时,![]()
其中正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
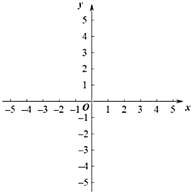
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com