
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60m,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1m,HF段的长为1.50m,篮板底部支架HE的长为0.75m.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1 m;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
【答案】(1)∠FHE=60°;(2)篮板顶端 F 到地面的距离是 4.4 米.
【解析】
(1)直接利用锐角三角函数关系得出cos∠FHE=![]() ,进而得出答案;
,进而得出答案;
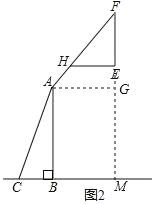
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,解直角三角形即可得到结论.
(1 )由题意可得:cos∠FHE=![]() ,则∠FHE=60°;
,则∠FHE=60°;
(2)延长 FE 交 CB 的延长线于 M,过 A 作 AG⊥FM 于 G,
在 Rt△ABC 中,tan∠ACB=![]() ,
,
∴AB=BCtan75°=0.60×3.732=2.2392,
∴GM=AB=2.2392,
在 Rt△AGF 中,∵∠FAG=∠FHE=60°,sin∠FAG=![]() ,
,
∴sin60°=![]() =
=![]() ,
,
∴FG≈2.17(m),
∴FM=FG+GM≈4.4(米),
答:篮板顶端 F 到地面的距离是 4.4 米.


科目:初中数学 来源: 题型:
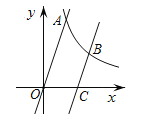
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于点
相交于点![]() (点
(点![]() 在第一象限),其横坐标为2.
在第一象限),其横坐标为2.
(1)求![]() 的值;
的值;
(2)若两个图像在第三象限的交点为![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
(3)点![]() 为此反比例函数图像上一点,其纵坐标为3,过点
为此反比例函数图像上一点,其纵坐标为3,过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
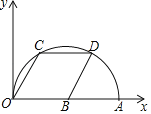
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点C、D在以OA为直径的半圆上,点B在OA上,且四边形OCDB是菱形,则点C的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
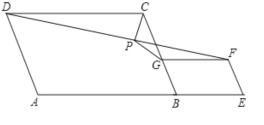
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A、 B、 E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
(1)如图①,在边长为8的等边三角形ABC中,点D,E分别在BC与AC上,且BD=2,∠ADE=60°,则线段CE的长为 .
问题
(2)如图②,已知AP∥BQ,∠A=∠B=90°,AB=6,D是射线AP上的一个动点(不与点A重合),E是线段AB上的一个动点(不与A,B重合),EC⊥DE,交射线BQ于点C,且AD+DE=AB,求△BCE的周长.
问题解决:
(3)如图③,在四边形ABCD中,AB+CD=10(AB<CD),BC=6,点E为BC的中点,且∠AED=108°,则边AD的长是否存在最大值?若存在,请求AD的最大值,并求出此时AB,CD的长度,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=6x+6与x轴、y轴分别交于A、D两点,直线l2:y=﹣x+3与x轴、y轴分别交于B、C两点.
(1)在直线l2上找一点E,使|AE﹣DE|的值最大,并求|AE﹣DE|的最大值.
(2)以AB为边作矩形ABMN,点C在边MN上,动点P从B出发,沿射线BM方向移动,作△PAB关于直线PA的对称△PAB'.是否存在点P,使得△PMB'是直角三角形?若存在,请直接写出所有符合题意的点P的坐标?若不存在,请说明理由.
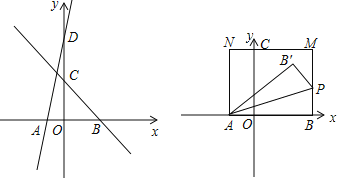
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com