
【题目】如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

科目:初中数学 来源: 题型:
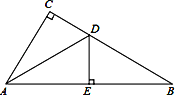
【题目】已知:如图 ,AD 是∠BAC 的平分线,且 DF⊥AC 于 F,∠B=90°,DE=DC.

(1)求证:BE=CF.
(2)若△ADE 和△DCF 的面积分别是12和5,求△ABC 的面积.
(3)请你写出∠BAC与∠CDE有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对任意一个两位数![]() ,如果
,如果![]() 满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为
满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为![]() .例如:
.例如:![]() ,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以
,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以![]() .根据以上定义,回答下列问题:
.根据以上定义,回答下列问题:
(1)填空:①下列两位数:40,42,44中,“迥异数”为_______;②计算:![]() =_______;
=_______;
(2)如果一个“迥异数”![]() 的十位数字是
的十位数字是![]() ,个位数字是
,个位数字是![]() ,且
,且![]() ,请求出“迥异数”
,请求出“迥异数”![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的20个小球,其中红球6个,黑球14个
(1)先从袋子中取出x(x>3)个红球后,再从袋子中随机摸出1个球,将“摸出黑球”,记为事件A.请完成下列表格.
事件A | 必然事件 | 随机事件 |
x的值 |
(2)先从袋子中取出m个红球,再放入2m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com