
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
科目:初中数学 来源: 题型:
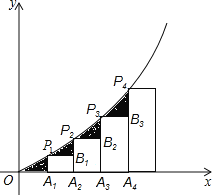
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市,l1 ,l2分别表示汽车、摩托车离A地的距离s(km)随时间t(h)变化的图象,则下列结论:①摩托车比汽车晚到1 h;②A,B两地的距离为20 km;③摩托车的速度为45 km/h,汽车的速度为60 km/h;④汽车出发1 h后与摩托车相遇,此时距离B地40 km;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
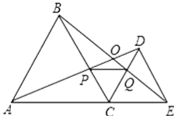
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④CO平分∠AOE;⑤∠AOB=60°.恒成立的结论有__.(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称

(1)画出△A1B1C1和△A2B2C2
(2)在x轴上确定一点P,使BP+A1P的值最小,直接写出P的坐标为________
(3)点Q在坐标轴上且满足△ACQ为等腰三角形,则这样的Q点有 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.

(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,直线l1∥x轴,直线l2为第一、三象限的角平分线,直线l1与l2相交于A(3,3),点B为直越l1上一点,点C为x轴上一点,P(x,y)为一动点.
(1)当点P(x,y)在x轴上时,y= ,当点P(x,y)在直线l1上,y= ,当点P(x,y)在直线l2上时y= .
如图1,当点P在直线l1下方、x轴上方、直线l2左上方区域时,x,y满足如下条件:![]() ,则∠APO,∠PAB,∠POC的数量关系是 .
,则∠APO,∠PAB,∠POC的数量关系是 .
如图2,当点P在直线l1下方、x轴上方、直线l2右下方区域时,x,y满足如下条件:![]() ,则∠APO,∠PAB,∠POC的数量关系是 .
,则∠APO,∠PAB,∠POC的数量关系是 .
(2)当点P在直线l1上方区域,且点P不在直线l2时,x,y满足的条件为:![]() ,请画出图形,猜想∠APO,∠PAB,∠POC的数量关系,并说明理由.
,请画出图形,猜想∠APO,∠PAB,∠POC的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
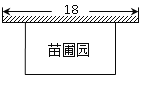
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
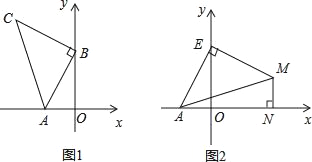
【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com