
分析 (1)直接利用有理数的乘方运算法则以及负整数指数幂的性质以及零指数幂的性质分别化简求出答案;
(2)直接利用积的乘方运算法则结合整式乘除运算法则化简,求出答案;
(3)首先利用乘法公式化简进而将已知数据代入求出答案;
(4)直接利用平方差公式将原式变形进而求出答案.
解答 解:(1)(-1)2015+($\frac{1}{3}$)-3-(π-3.1)0
=-1+$\frac{1}{(\frac{1}{3})^{3}}$-1
=-1+27-1
=25;
(2)(-2x2y)2•3xy÷(-6x2y)
=4x4y2•3xy÷(-6x2y)
=12x5y3÷(-6x2y)
=-2x3y2;
(3)[(2x+y)2+(2x+y)(y-2x)-6y]÷2y,
=(4x2+4xy+y2+y2-4x2-6y)÷2y
=(4xy+2y2-6y)÷2y
=2x+y-3
把x=-$\frac{1}{2}$,y=3代入得:
原式=2×(-$\frac{1}{2}$)+3-3=-1;
(4)$\frac{15{6}^{2}-15{4}^{2}}{201{6}^{2}-2015×2017}$
=$\frac{(156-154)(156+154)}{201{6}^{2}-(2016-1)(2016+1)}$
=$\frac{2×310}{201{6}^{2}-201{6}^{2}+1}$
=620.
点评 此题主要考查了实数运算以及整式的混合运算和化简求值,熟练应用乘法公式是解题关键.


科目:初中数学 来源: 题型:选择题
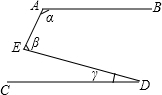 如图,AB∥CD,图中α、β、γ三个角之间的数量关系为( )
如图,AB∥CD,图中α、β、γ三个角之间的数量关系为( )| A. | α+β+γ=360° | B. | α+β-γ=180° | C. | α+β+γ=180° | D. | α-β-γ=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=c2-b2 | B. | a=6,b=10,c=8 | ||
| C. | ∠A:∠B:∠C=3:4:5 | D. | a=8k,b=17k,c=15k |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.
如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$是8的算术平方根 | B. | 2<$\sqrt{8}$<3 | ||
| C. | $\sqrt{8}$=$±2\sqrt{2}$ | D. | $\sqrt{8}$是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
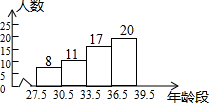 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )| A. | 平均年龄是37.5岁 | B. | 中位数年龄位于33.5-36.5岁 | ||
| C. | 众数年龄位于36.5-39.5岁 | D. | 以上选项都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
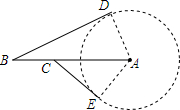 如图所示,某海域直径为30n mile的暗礁区中心有一哨所A,值班人员发现有一轮船从哨所的正西方向90n mile的B处向哨所驶来,哨所及时向轮船发出了危险信号,但轮船没有收到信号,又继续前进了15n mile到达C处,此时哨所第二次发出紧急信号.
如图所示,某海域直径为30n mile的暗礁区中心有一哨所A,值班人员发现有一轮船从哨所的正西方向90n mile的B处向哨所驶来,哨所及时向轮船发出了危险信号,但轮船没有收到信号,又继续前进了15n mile到达C处,此时哨所第二次发出紧急信号.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com