【题目】某体育用品商店购进乒乓球拍和羽毛球拍进行销售，已知羽毛球拍比乒乓球拍每副进价高20元，用10000元购进羽毛球拍与用8000元购进乒乓球拍的数量相等.
（1）求每副乒乓球拍、羽毛球拍的进价各是多少元？
（2）该体育用品商店计划用不超过8840元购进乒乓球拍、羽毛球拍共100副进行销售，且乒乓球拍的进货量不超过60副，请求出该商店有几种进货方式？
【答案】（1）每副乒乓球拍、羽毛球拍进价分别为80元、100元；（2）共有3种进货方式，详见解析.
【解析】
（1）可设购买1副乒乓球拍需x元，根据用10000元购进羽毛球拍与用8000元购进乒乓球拍的数量相等，列出分式方程，解方程检验即可.
（2）可设购买了乒乓球拍y副，根据该体育用品商店计划用不超过8840元购进乒乓球拍、羽毛球拍共100副，列出不等式求解，再根据乒乓球拍的进货量不超过60副取公共部分的整数，可知共有3种.
（1）设每副乒乓球拍进价为x元，由题意得：
解得:
，
经检验是原方程的解,且符合题意，
此时
.
答：每副乒乓球拍、羽毛球拍进价分别为80元、100元.
（2）设购进乒乓球拍y副，由题意得：
解得：
，
因为
所以
，
所以
.
故共有3种进货方式：
①购买58副乒乓球拍，42副羽毛球拍；
②购买59副乒乓球拍，41副羽毛球拍；
③购买60副乒乓球拍，40副羽毛球拍．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B＞90°，CD为∠ACB的角平分线，在AC边上取点E，使DE＝DB，且∠AED＞90°．若∠A＝α，∠ACB＝β，则（ ）
A.∠AED＝180°﹣α﹣βB.∠AED＝180°﹣α﹣
β
C.∠AED＝90°﹣α+βD.∠AED＝90°+α+β
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一条公路上顺次有
、
、
三地，甲、乙两车同时从地出发，分别匀速前柱地、地，甲车到达地停留一段时间后原速原路返回，乙车到达地后立即原速原路返回（掉头时间忽略不计），乙车比甲车早1小时返回地，甲、乙两车各自行驶的路程
（千米）与时间
（时）（从两车出发时开始计时）之间的变化情况如图所示.
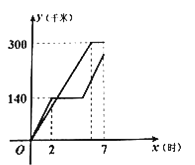
（1）在这个变化过程中，自变量是______，因变量是______.
（2）甲车到达地停留的时长为______小时，乙车从出发到返回地共用了______小时.
（3）甲车的速度是______千米/时，乙车的速度是______千米/时.
（4）、两地相距______千米，甲车返回地途中与之间的关系式是______（不必写出自变量取值范围）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD 边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有（ ）
A. 4次 B. 3次 C. 2次 D. 1次
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】基本图形：在RT△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE．
探索：（1）连接EC，如图①，试探索线段BC，CD，CE之间满足的等量关系，并证明结论；
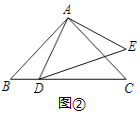
（2）连接DE，如图②，试探索线段DE，BD，CD之间满足的等量关系，并证明结论；
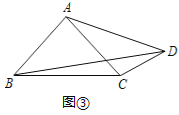
联想：（3）如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°，若BD=7，CD=2，则AD的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
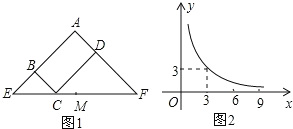
【题目】图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的序号是___.①当x=3时，EC<EM；②当y=9时，EC>EM③当x增大时，ECCF的值增大；④当y增大时，BEDF的值不变。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为
万元/辆，经销一段时间后发现：当该型号汽车售价定为
万元/辆时，平均每周售出
辆；售价每降低
万元，平均每周多售出
辆.
（1）当售价为
万元/辆时，平均每周的销售利润为___________万元；
（2）若该店计划平均每周的销售利润是
万元，为了尽快减少库存，求每辆汽车的售价．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
