
【题目】如图,在△ABC中,AB=AC=4,P为BC边上任意一点.
(1)求证:AP2+PB·PC=16.
(2)若BC边上有100个不同的点(不与点B,C重合)P1,P2,…,P100,设mi=APi2+PiB·PiC(i=1,2,…,100).求m1+m2+…+m100的值.
【答案】(1)16;(2)1600
【解析】试题分析:(1)作AD⊥BC于D,由等腰三角形的三线合一性质和勾股定理得出AP2+BPPC=AB2即可;
(2)根据勾股定理,得APi2=AD2+DPi2=AD2+(BD-BPi)2=AD2+BD2-2BDBPi+BPi2,PiBPiC=PiB(BC-PiB)=2BDBPi-BPi2,从而求得mi=AD2+BD2,即可求解.
试题解析:
(1)过点A作AD⊥BC于点D.
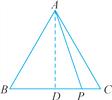
∵AB=AC,AD⊥BC,
∴BD=CD,∠ADB=∠ADC=90°,
∴AP2+PB·PC=AP2+(PD+BD)(CD-PD)=AP2+CD2-PD2.
∵AP2-PD2=AD2,
∴AP2+PB·PC=AD2+CD2=AC2=16.
(2)由(1)知mi=APi2+PiB·PiC=16,
∴m1=m2=…=m100=16,
∴m1+m2+…+m100=16×100=1600.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.

根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a= 人,其中选择“绘画”的学生人数占抽样人数的百分比为b= ;
(2)补全条形统计图;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
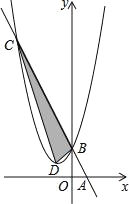
A.8:1 B.6:1 C.5:1 D.4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年5月某日我国部分城市的最高气温统计如下表所示:
城 市 | 武汉 | 成都 | 北京 | 上海 | 海南 | 南京 | 拉萨 | 深圳 |
气温(℃) | 27 | 27 | 24 | 25 | 28 | 28 | 23 | 26 |
请问这组数据的平均数是( )
A.24 B.25 C.26 D.27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com