
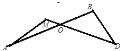
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖĻ߶ĪAB”¢CDĻą½»ÓŚµćO£¬Į¬½ÓAC”¢BD£¬ŌņĪŅĆĒ°ŃŠĪČēÕāŃłµÄĶ¼ŠĪ³ĘĪŖ”°8×ÖŠĶ”±£®
(1)ĒóÖ¤£ŗ”ĻA+”ĻC£½”ĻB+D£»
(2)ČēĶ¼2£¬Čō”ĻCABŗĶ”ĻBDCµÄĘ½·ÖĻßAPŗĶDPĻą½»ÓŚµćP£¬ĒŅÓėCD”¢AB·Ö±šĻą½»ÓŚµćM”¢N£®
¢ŁŅŌĻ߶ĪACĪŖ±ßµÄ”°8×ÖŠĶ”±ÓŠ”” ””øö£¬ŅŌµćOĪŖ½»µćµÄ”°8×ÖŠĶ”±ÓŠ”” ””øö£»
¢ŚČō”ĻB£½100”ć£¬”ĻC£½120”ć£¬Ēó”ĻPµÄ¶ČŹż£»
¢ŪČō½ĒĘ½·ÖĻßÖŠ½ĒµÄ¹ŲĻµøÄĪŖ”°”ĻCAP£½![]() ”ĻCAB£¬”ĻCDP£½
”ĻCAB£¬”ĻCDP£½![]() ”ĻCDB”±£¬ŹŌĢ½¾æ”ĻPÓė”ĻB”¢”ĻCÖ®¼ä“ęŌŚµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ĄķÓÉ£®
”ĻCDB”±£¬ŹŌĢ½¾æ”ĻPÓė”ĻB”¢”ĻCÖ®¼ä“ęŌŚµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ĄķÓÉ£®

”¾“š°ø”æ(1)Ö¤Ć÷¼ū½āĪö£»(2)¢Ł3£¬ 4£»¢Ś”ĻP£½110”ć£»¢Ū3”ĻP£½”ĻB+2”ĻC£¬ĄķÓɼū½āĪö.
”¾½āĪö”æ
(1)ÓÉČż½ĒŠĪÄŚ½ĒŗĶµĆµ½”ĻA+”ĻC=180”ć©”ĻAOC£¬”ĻB+”ĻD=180”ć©”ĻBOD£¬ÓɶŌ¶„½ĒĻąµČ£¬µĆµ½”ĻAOC=”ĻBOD£¬Ņņ¶ų”ĻA+”ĻC=”ĻB+”ĻD£»
(2)¢ŁŅŌĻ߶ĪACĪŖ±ßµÄ”°8×ÖŠĪ”±ÓŠ3øö£¬ŅŌOĪŖ½»µćµÄ”°8×ÖŠĪ”±ÓŠ4øö£»
¢Śøł¾Ż(1)µÄ½įĀŪ£¬ŅŌMĪŖ½»µć”°8×ÖŠĶ”±ÖŠ£¬”ĻP+”ĻCDP£½”ĻC+”ĻCAP£¬ŅŌNĪŖ½»µć”°8×ÖŠĶ”±ÖŠ£¬”ĻP+”ĻBAP£½”ĻB+”ĻBDP£¬Į½µČŹ½Ļą¼ÓµĆµ½2”ĻP+”ĻBAP+”ĻCDP=”ĻB+”ĻC+”ĻCAP+”ĻBDP£¬ÓÉAPŗĶDPŹĒ½ĒĘ½·ÖĻߣ¬µĆµ½”ĻBAP£½”ĻCAP£¬”ĻCDP£½”ĻBDP£¬“Ó¶ų”ĻP=![]() (”ĻB+”ĻC)£¬Č»ŗ󽫔ĻB=100£¬”ĻC=120“śČė¼ĘĖć¼“æÉ£»
(”ĻB+”ĻC)£¬Č»ŗ󽫔ĻB=100£¬”ĻC=120“śČė¼ĘĖć¼“æÉ£»
¢ŪÓė¢ŚµÄÖ¤Ć÷·½·ØŅ»ŃłµĆµ½3”ĻP=”ĻB+2”ĻC.
½ā£ŗ(1)ŌŚĶ¼1ÖŠ£¬ÓŠ”ĻA+”ĻC£½180”ć©”ĻAOC£¬”ĻB+”ĻD£½180”ć©”ĻBOD£¬
”ß”ĻAOC£½”ĻBOD£¬
”ą”ĻA+”ĻC£½”ĻB+”ĻD£»
(2)½ā£ŗ¢ŁŅŌĻ߶ĪACĪŖ±ßµÄ”°8×ÖŠĶ”±ÓŠ3øö£ŗ
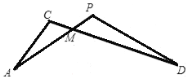
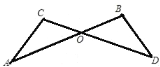

ŅŌµćOĪŖ½»µćµÄ”°8×ÖŠĶ”±ÓŠ4øö£ŗ
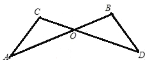

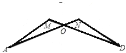
¢ŚŅŌMĪŖ½»µć”°8×ÖŠĶ”±ÖŠ£¬ÓŠ”ĻP+”ĻCDP£½”ĻC+”ĻCAP£¬
ŅŌNĪŖ½»µć”°8×ÖŠĶ”±ÖŠ£¬ÓŠ”ĻP+”ĻBAP£½”ĻB+”ĻBDP
”ą2”ĻP+”ĻBAP+”ĻCDP£½”ĻB+”ĻC+”ĻCAP+”ĻBDP£¬
”ßAP”¢DP·Ö±šĘ½·Ö”ĻCABŗĶ”ĻBDC£¬
”ą”ĻBAP£½”ĻCAP£¬”ĻCDP£½”ĻBDP£¬
”ą2”ĻP£½”ĻB+”ĻC£¬
”ß”ĻB£½100”ć£¬”ĻC£½120”ć£¬
”ą”ĻP£½![]() £Ø”ĻB+”ĻC£©=
£Ø”ĻB+”ĻC£©=![]() £Ø100”ć+120”ć£©£½110”ć£»
£Ø100”ć+120”ć£©£½110”ć£»
¢Ū3”ĻP£½”ĻB+2”ĻC£¬ĘäĄķÓÉŹĒ£ŗ
”ß”ĻCAP£½![]() ”ĻCAB£¬”ĻCDP£½
”ĻCAB£¬”ĻCDP£½![]() ”ĻCDB£¬
”ĻCDB£¬
”ą”ĻBAP£½![]() ”ĻCAB£¬”ĻBDP£½
”ĻCAB£¬”ĻBDP£½![]() ”ĻCDB£¬
”ĻCDB£¬
ŅŌMĪŖ½»µć”°8×ÖŠĶ”±ÖŠ£¬ÓŠ”ĻP+”ĻCDP£½”ĻC+”ĻCAP£¬
ŅŌNĪŖ½»µć”°8×ÖŠĶ”±ÖŠ£¬ÓŠ”ĻP+”ĻBAP£½”ĻB+”ĻBDP
”ą”ĻC©”ĻP£½”ĻCDP©”ĻCAP£½![]() £Ø”ĻCDB©”ĻCAB£©£¬
£Ø”ĻCDB©”ĻCAB£©£¬
”ĻP©”ĻB£½”ĻBDP©”ĻBAP£½![]() £Ø”ĻCDB©”ĻCAB£©£®
£Ø”ĻCDB©”ĻCAB£©£®
”ą2£Ø”ĻC©”ĻP£©£½”ĻP©”ĻB£¬
”ą3”ĻP£½”ĻB+2”ĻC£®
¹Ź“š°øĪŖ£ŗ(1)Ö¤Ć÷¼ū½āĪö£»(2)¢Ł3£¬ 4£»¢Ś”ĻP£½110”ć£»¢Ū3”ĻP£½”ĻB+2”ĻC£¬ĄķÓɼū½āĪö.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ·“±ČĄżŗÆŹż ![]() £¬ŌņĻĀĮŠ½įĀŪ²»ÕżČ·µÄŹĒ( )
£¬ŌņĻĀĮŠ½įĀŪ²»ÕżČ·µÄŹĒ( )
A.Ķ¼Ļó±Ų¾¹żµć£Ø-1£¬5£©
B.Ķ¼ĻóµÄĮ½øö·ÖÖ§·Ö²¼ŌŚµŚ¶ž”¢ĖÄĻóĻŽ
C.yĖęxµÄŌö“ó¶ųŌö“ó
D.Čōx£¾1£¬Ōņ£5£¼y£¼0
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒÖŖµĄ£¬ÓŠĄķŹż°üĄØÕūŹż”¢ÓŠĻŽŠ”ŹżŗĶĪŽĻŽŃ»·Š”Źż£¬ŹĀŹµÉĻ£¬ĖłÓŠµÄÓŠĄķŹż¶¼æÉŅŌ»ÆĪŖ·ÖŹżŠĪŹ½(ÕūŹżæÉæ“×÷·ÖÄøĪŖ1µÄ·ÖŹż)£¬ÄĒĆ“ĪŽĻŽŃ»·Š”ŹżČēŗĪ±ķŹ¾ĪŖ·ÖŹżŠĪŹ½ÄŲ£æĒėæ“ŅŌĻĀŹ¾Ąż£ŗ
Ąż£ŗ½«![]() »ÆĪŖ·ÖŹżŠĪŹ½£¬
»ÆĪŖ·ÖŹżŠĪŹ½£¬
ÓÉÓŚ![]() £¬Éč
£¬Éč![]() £¬¢Ł
£¬¢Ł
µĆ![]() £¬¢Ś
£¬¢Ś
¢Ś¢ŁµĆ![]() ,½āµĆ
,½āµĆ![]() ,ÓŚŹĒµĆ
,ÓŚŹĒµĆ![]() .
.
Ķ¬ĄķæɵĆ![]() ,
,![]() .
.
øł¾ŻŅŌÉĻŌĶĮ,»Ų“šĻĀĮŠĪŹĢā£ŗ(ŅŌĻĀ¼ĘĖć½į¹ū¾łÓĆ×ī¼ņ·ÖŹż±ķŹ¾)
£ØĄą±ČÓ¦ÓĆ£©
(1)![]() £»
£»
(2)½«![]() »ÆĪŖ·ÖŹżŠĪŹ½£¬Š“³öĶʵ¼¹ż³Ģ£»
»ÆĪŖ·ÖŹżŠĪŹ½£¬Š“³öĶʵ¼¹ż³Ģ£»
£ØĒØŅĘĢįÉż£©
(3)![]() £¬
£¬![]() £»(×¢
£»(×¢![]() ,
,![]() £©
£©
£ØĶŲÕ¹·¢ĻÖ£©
(4)ČōŅŃÖŖ![]() £¬Ōņ
£¬Ōņ![]() .
.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży£½ax2£«bx£«c(a”Ł0)µÄĶ¼ĻóÓėxÖį½»ÓŚA£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬ĒŅOA£½OC.ŌņĻĀĮŠ½įĀŪ£ŗ¢Łabc£¼0£»¢Ś ![]() £»¢Ūac£b£«1£½0£»¢ÜOA”¤OB£½
£»¢Ūac£b£«1£½0£»¢ÜOA”¤OB£½ ![]() .ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©
.ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©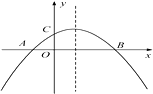
A.4
B.3
C.2
D.1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬BDĪŖÕż·½ŠĪABCDµÄ¶Ō½ĒĻߣ¬BEĘ½·Ö”ĻDBC£¬½»DCÓėµćE£¬½«”÷BCEČʵćCĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½”÷DCF£¬ČōCE£½1 cm£¬ŌņBF£½cm.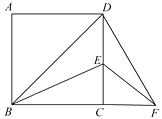
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßl1£ŗy1£½©![]() x+b·Ö±šÓėxÖį”¢yÖį½»ÓŚµćA”¢µćB£¬ÓėÖ±Ļßl2£ŗy2£½x½»ÓŚµćC£Ø2£¬2£©£®
x+b·Ö±šÓėxÖį”¢yÖį½»ÓŚµćA”¢µćB£¬ÓėÖ±Ļßl2£ŗy2£½x½»ÓŚµćC£Ø2£¬2£©£®
£Ø1£©Čōy1£¼y2£¬ĒėÖ±½ÓŠ“³öxµÄȔֵ·¶Ī§£»
£Ø2£©µćPŌŚÖ±Ļßl1£ŗy1£½©![]() x+bÉĻ£¬ĒŅ”÷OPCµÄĆ껿ĪŖ3£¬ĒóµćPµÄ×ų±ź£æ
x+bÉĻ£¬ĒŅ”÷OPCµÄĆ껿ĪŖ3£¬ĒóµćPµÄ×ų±ź£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠŅ»Åś¹²Ļķµ„³µŠčŅŖĪ¬ŠŽ£¬Ī¬ŠŽŗó¼ĢŠųĶ¶·ÅĘļÓĆ£¬ĻÖÓŠ¼×”¢ŅŅĮ½ČĖ×öĪ¬ŠŽ£¬¼×ĆæĢģĪ¬ŠŽ16Į¾£¬ŅŅĆæĢģĪ¬ŠŽµÄ³µĮ¾±Č¼×¶ą8Į¾£¬¼×µ„¶ĄĪ¬ŠŽĶź³ÉÕāÅś¹²Ļķµ„³µ±ČŅŅµ„¶ĄĪ¬ŠŽĶź¶ąÓĆ20Ģģ£¬¹«Ė¾ĆæĢģø¶¼×80ŌŖĪ¬ŠŽ·Ń£¬ø¶ŅŅ120ŌŖĪ¬ŠŽ·Ń£®
£Ø1£©ĪŹŠčŅŖĪ¬ŠŽµÄÕāÅś¹²Ļķµ„³µ¹²ÓŠ¶ąÉŁĮ¾£æ
£Ø2£©ŌŚĪ¬ŠŽ¹ż³ĢÖŠ£¬¹«Ė¾ŅŖÅÉŅ»ĆūČĖŌ±½ųŠŠÖŹĮæ¼ą¶½£¬¹«Ė¾øŗµ£ĖūĆæĢģ10ŌŖ²¹Öś·Ń£¬ĻÖÓŠČżÖÖĪ¬ŠŽ·½°ø£ŗ¢ŁÓɼ׵„¶ĄĪ¬ŠŽ£»
¢ŚÓÉŅŅµ„¶ĄĪ¬ŠŽ£»
¢Ū¼×”¢ŅŅŗĻ×÷Ķ¬Ź±Ī¬ŠŽ£¬ÄćČĻĪŖÄÄÖÖ·½°ø×īŹ”Ē®£¬ĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×ŅŅĮ½Ķ¬Ń§ÓĆŅ»ø±ĘĖæĖÅĘÖŠÅĘĆꏿ×Ö·Ö±šŹĒ3£¬4£¬5£¬6µÄ4ÕÅÅĘ×ö³éŹż×ÖÓĪĻ·£¬ÓĪĻ·¹ęŌņŹĒ£ŗ½«Õā4ÕÅÅʵÄÕżĆęČ«²æ³ÆĻĀ£¬Ļ“ŌČ£¬“ÓÖŠĖ껜³éČ”Ņ»ÕÅ£¬³éµĆµÄŹż×÷ĪŖŹ®Ī»ÉĻµÄŹż×Ö£¬³é³öµÄÅĘ²»·Å»Ų£¬Č»ŗó½«Ź£ĻĀµÄÅĘĻ“ŌČ£¬ŌŁ“ÓÖŠĖ껜³éČ”Ņ»ÕÅ£¬³éµĆµÄŹż×÷ĪŖøöĪ»ÉĻµÄŹż×Ö£¬ÕāŃł¾ĶµĆµ½Ņ»øöĮ½Ī»Źż£¬ČōÕāøöĮ½Ī»ŹżŠ”ÓŚ45£¬Ōņ¼×»ńŹ¤£¬·ńŌņŅŅ»ńŹ¤£®ÄćČĻĪŖÕāøöÓĪĻ·¹«Ę½Āš£æĒėĄūÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
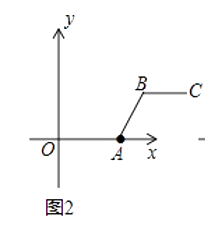
”¾ĢāÄæ”æ¶ØŅå£ŗP”¢Q·Ö±šŹĒĮ½ĢõĻ߶Īa£¬bÉĻČĪŅāŅ»µć£¬Ļ߶ĪPQ³¤¶ČµÄ×īŠ”Öµ½Š×öĻ߶ĪaÓėĻ߶ĪbµÄ¾ąĄė£®ŅŃÖŖ£¬O£Ø0£¬0£©£¬A£Ø4£¬0£©£¬B£Øm£¬n£©£¬C£Øm+4£¬n£©ŹĒĘ½ĆęÖ±½Ē×ų±źĻµÖŠĖÄµć£®
£Ø1£©øł¾ŻÉĻŹö¶ØŅ壬µ±m=2£¬n=2Ź±£¬ČēĶ¼1£¬Ļ߶ĪBCÓėĻ߶ĪOAµÄ¾ąĄėĪŖ£»µ±m=5£¬n=2Ź±£¬ČēĶ¼2£¬Ļ߶ĪBCÓėĻ߶ĪOAµÄ¾ąĄė£Ø¼“Ļ߶ĪABµÄ³¤£©ĪŖ£»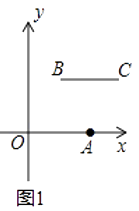
£Ø2£©ČēĶ¼3£¬ČōµćBĀäŌŚŌ²ŠÄĪŖA£¬°ė¾¶ĪŖ2µÄŌ²ÉĻ£¬Ļ߶ĪBCÓėĻ߶ĪOAµÄ¾ąĄė¼ĒĪŖd£¬Ēód¹ŲÓŚmµÄŗÆŹż½āĪöŹ½£®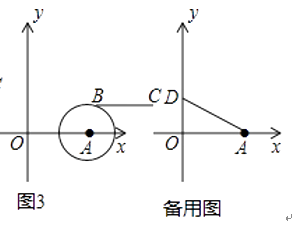
£Ø3£©µ±mÖµ±ä»ÆŹ±£¬¶ÆĻ߶ĪBCÓėĻ߶ĪOAµÄ¾ąĄėŹ¼ÖÕĪŖ2£¬Ļ߶ĪBCµÄÖŠµćĪŖM£¬µćD£Ø0£¬2£©£¬m”Ż0£¬n”Ż0£¬×÷MH”ĶxÖį£¬“¹×ćĪŖH£¬ŹĒ·ń“ęŌŚmÖµ£¬Ź¹ŅŌA”¢M”¢HĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AODĻąĖĘ£æČō“ęŌŚ£¬Ēó³ömÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com