Question

1．在⊙O中，AB为直径，点P在AB的延长线上，PC与⊙相切于点C，点D为$\widehat{AC}$上的点，且$\widehat{AD}$=$\widehat{BC}$，连接AD．
（1）如图1，求证：2∠A-∠P=90°；
（2）如图2，延长AD、PC交于点E，若∠E=90°，求证：PC=$\sqrt{3}$AD；
（3）如图3，延长AD、PC交于点E，点F在AO上，连接DF、CF，∠ECF=∠AFD-∠CFP，DF=2，AB=6，求线段CF的长．

Answer 1

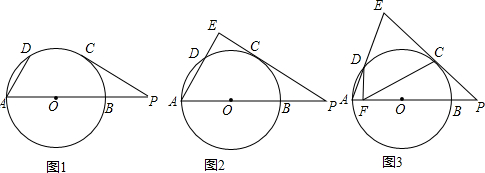
分析 （1）先由切线得出∠POC=90°-∠P，再由两弧相等得出∠AOD=∠POC，最后用三角形的内角和为180°即可得出结论；
（2）先判断出OC∥AD得出∠POC=∠A，借助（1）结论求出∠P=30°，得出PC=$\sqrt{3}$OC，再判断出四边形AOCD是平行四边形，即可得出结论；
（3）先由切线的性质和折叠的性质∠ECF=∠NHF，再结合已知得出∠GFH=∠NHF，用CD∥AB，得出∠DCH=90°，即DH是⊙O的直径，进而得出∠FGH是直角，再用
等角的余角相等得出∠FHG=∠FHD，进而用角平分线定理得出HG=3GF，在直角三角形DGH中，用勾股定理求出GF，HG，即可求出HD即可．

解答 解：（1）如图1，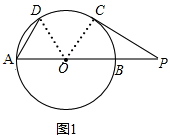

连接OC，OD，
∵PC是⊙O的切线，
∴∠OCP=90°，
∴∠POC=90°-∠P，
∵$\widehat{AD}$=$\widehat{BC}$，
∴∠AOD=∠POC，
∴∠AOD=90°-∠P，
∵OA=OD，
∴∠A=∠ADO
∴∠AOD+∠A+∠ADO=180°，
∴90°-∠P+2∠A=180°，
∴2∠A-∠P=90°，
（2）如图2，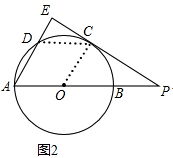

连接OC，CD，
∵PC是⊙O的切线，
∴∠PCO=90°，
∵∠E=90°，
∴∠PCO=∠E，
∴OC∥AC，
∴∠POC=∠A，
在Rt△POC中，∠P+∠POC=90°，
∴∠A+∠P=90°，
由（1）知，2∠A-∠P=90°，
∴∠P=30°，
∴PC=$\sqrt{3}$OC
∵$\widehat{AD}$=$\widehat{BC}$，
∴CD∥AB，
∵OC∥AE，
∴四边形AOCD是平行四边形，
∴OC=AD，
∴PC=$\sqrt{3}$AD；
（3）如图3，过点C作CH⊥AB于M，连接CD，FH，DH，延长DF，PH相交于点N，连接CG，HG，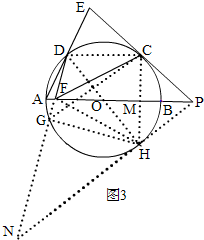

∵CH⊥AB，
∴∠FCH=∠FHC，∠CFB=∠HFB，
∵∠ECF=∠AFD-∠CFP，
∴∠GFH=∠ECH，
∵PC，PH于⊙O相切，
∴∠PCH=∠PHC，
∴∠PCH+∠FCH=∠PHC+∠FHC，
∴∠PCF=∠PHF，
∴∠ECF=∠NHF，
∵∠GFH=∠ECH，
∴∠GFH=∠NHF，
∴$\widehat{AD}=\widehat{BC}$，
∴CD∥AB，
∴∠CMA=90°，
∴∠DCH=90°，
∴DH是⊙O的直径，
∴∠DGH=90°
∴∠FHG=90°-∠GFH=90°-∠FHN，
∵DH是⊙O直径，
∴∠DHN=90°，
∴∠FHD=90°-∠FHN，
∴∠FHG=∠FHD，
∴$\frac{DH}{HG}=\frac{DF}{FG}$，
∵AB=DH=6，FD=2
∴$\frac{6}{HG}=\frac{2}{FG}$，
∴HG=3GF，
在Rt△DGH中，HG²+DG²=HD²，
∴9GF²+（2+GF）²=36，
∴GF=$\frac{8}{5}$，
∴FH=$\sqrt{H{G}^{2}+G{F}^{2}}$=$\sqrt{10}$GF=$\frac{8}{5}\sqrt{10}$．
∵CH⊥HB，
∴CF=FH=$\frac{8}{5}\sqrt{10}$．

点评 此题是圆的综合题，主要考查了切线的性质，等弧所对的圆心角相等，平行线的性质和判定，平行四边形的判定和性质，折叠的性质，勾股定理，角平分线定理，解本题的关键是得出∠FHG=∠FHD，也是解本题的难点，由∠ECF=∠AFD-∠CFP作辅助线也是解本题难点，是一道难点比较大的综合题．