Question

列方程解应用题：在九台市城市道路改造中，决定对一段公路进硬化，已知这项工程由甲队做要40天完成，如果由乙队先做10天，余下的工程由两队合做还要20天才能完成．
（1）求乙队单独完成这项工程所需天数．
（2）两队合作完成全部工程所需天数．

Answer 1

解：（1）设乙队单独完成这项工作需x天．
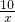
+（+）×20=1，
解得：x=60，
经检验得出x=60是原方程的解，且符合题意，
答：乙队单独完成这项工程需60天．

（2）设两队合做完成这项工程所需的天数为y天，
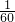
根据题意得：1÷（+）=24（天），
答：两队合作完成全部工程需24天．
分析：（1）等量关系为：工作时间=工作总量÷工作效率，根据题意可得出：甲队的总工作量+乙队的总工作量=1，由此可列出方程求解；
（2）根据1除以甲乙工作效率之和即为两队合做完成这项工程所需的天数．
点评：本题主要考查分式方程的应用培养学生对方程知识的应用能力，利用相应的工作量的等量关系来解决相关问题是解题关键．