
����Ŀ��һ���߲˹�˾�չ���ij����ɫ�߲�140�֣����ӹ���������ۣ����ۺ������������ʾ��
���۷�ʽ | �ּӹ������� | ���ӹ������� |
ÿ�ֻ�����Ԫ�� | 1000 | 2000 |
��֪�ù�˾�ļӹ������ǣ�ÿ���ܾ��ӹ�5�ֻ�ּӹ�15�֣������ּӹ�����ͬʱ���У��ܼ��ڵ����������ƣ���˾������һ��ʱ���ڽ������߲�ȫ���ӹ��������꣮
��1�����Ҫ��12��պüӹ���140���߲ˣ���˾Ӧ���ż��쾫�ӹ�������ּӹ���
��2������Ƚ��о��ӹ���Ȼ����дּӹ��� ���������������WԪ�뾫�ӹ����߲˶���m֮��ĺ�����ϵʽ��
����Ҫ���ڲ�����10���ʱ���ڣ���140���߲�ȫ���ӹ����������ۣ���ӹ������߲�����ö�������ʱ��η���ӹ�ʱ�䣿
���𰸡�
��1���⣺��Ӧ����x����о��ӹ���y����дּӹ���
��������� ![]() ��
��
��� ![]() ��
��
��Ӧ����4����о��ӹ���8����дּӹ�
��2���⣺�پ��ӹ�m�֣���ּӹ���140��m���֣���������ã�
W=2000m+1000��140��m��
=1000m+140000��
�ڡ�Ҫ���ڲ�����10���ʱ���ڽ������߲˼ӹ��꣬
�� ![]() +
+ ![]() ��10��
��10��
��ã�m��5
��0��m��5��
�֡���һ�κ���W=1000m+140000�У�k=1000��0��
��W��m�����������
�൱m=5ʱ��W���=1000��5+140000=145000��
�ྫ�ӹ�����Ϊ5��5=1��
�ּӹ�����Ϊ��140��5����15=9��
�ల��1����о��ӹ���9����дּӹ������Ի���������Ϊ145000Ԫ
����������1�����������ϵΪ�����ӹ�����+�ּӹ�����=12�����ӹ�����+�ּӹ�����=140���г���������⼴�ɣ���2���ٸ��ݾ��ӹ������ʹּӹ������ĵ�����ϵ���þ��ӹ�����m����ʾ�ּӹ����������г�W��m֮��Ĺ�ϵ���ڸ�������Ҫ����ȷ��m��ȡֵ��Χ��Ȼ���ʾW�����W���ֵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB�����˵������ֱ�ΪA��6��6����B��8��2������ԭ��OΪλ�����ģ��ڵ�һ�����ڽ��߶�AB��СΪԭ���� ![]() ��õ��߶�CD�����B�Ķ�Ӧ��D������Ϊ�� ��
��õ��߶�CD�����B�Ķ�Ӧ��D������Ϊ�� �� 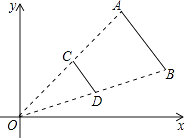
A.��3��3��
B.��1��4��
C.��3��1��
D.��4��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D�ڱ�BC�ϣ���AΪԲ�ģ�AD��Ϊ�뾶��Բ��������BC����һ��E������AC��F������AE��EF�� 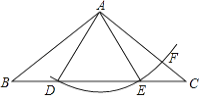
��1����֤����ABD�ա�ACE��
��2������ADB=3��CEF�����ж�EF��AB��������λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=BD����E��F�ֱ���AB��AD�ϣ���AE=DF������BF��DE�ཻ�ڵ�G������CG��BD�ཻ�ڵ�H�����н��ۣ� �١�AED�ա�DFB����S�ı���BCDG= ![]() CG2������AF=2DF����BG=6GF��
CG2������AF=2DF����BG=6GF��
������ȷ�Ľ��ۣ� ��
A.ֻ�Т٢�
B.ֻ�Т٢�
C.ֻ�Тڢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OΪԲ�ĵ�����ͬ��Բ�У�AB����Բ��O������СԲ�ཻ�ڵ�A�����Բ�ཻ�ڵ�B��СԲ������AC���Բ�ཻ�ڵ�D����COƽ�֡�ACB�� 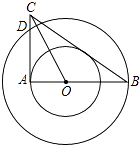
��1�����ж�BC����ֱ����СԲ��λ�ù�ϵ����˵�����ɣ�
��2�����ж��߶�AC��AD��BC֮���������ϵ����˵�����ɣ�
��3����AB=8��BC=10�����Բ��СԲΧ�ɵ�Բ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�͵�F����B�͵�E�ֱ��Ƿ���������y= ![]() ͼ���ڵ�һ���͵��������ϵĵ㣬����A��B��AC��x�ᣬBD��x�ᣬ����ֱ�Ϊ��C��D��CD=6����AF=FC��DE=BE����֪�ı���ADCF��������ı���BCDE�������2������OC�ij�Ϊ ��
ͼ���ڵ�һ���͵��������ϵĵ㣬����A��B��AC��x�ᣬBD��x�ᣬ����ֱ�Ϊ��C��D��CD=6����AF=FC��DE=BE����֪�ı���ADCF��������ı���BCDE�������2������OC�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ�˶��θ�ʽ�������������Ƿ���һЩ���и��ŵ�ʽ�ӿ��Ա�ʾ����һ��ʽ�ӵ�ƽ�����磺
3+2![]() ��2+2
��2+2![]() +1��(
+1��(![]() )2+2
)2+2![]() +1��(
+1��(![]() +1)2��
+1)2��
5+2![]() ��2+2
��2+2![]() +3��(
+3��(![]() )2+2��
)2+2��![]() ��
��![]() +(
+(![]() )2��(
)2��(![]() +
+![]() )2
)2
(1)���������ʽ�ӵı仯���̣������и�ʽ������һ��ʽ�ӵ�ƽ������ʽ��
��4+2![]() ����6+4
����6+4![]()
(2)��a+4![]() ��(m+n
��(m+n![]() )2����a��m��n����������������a��ֵ��
)2����a��m��n����������������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��Բ��ֱ������C�ǻ�AD���е㣬����C��BD�ӳ��ߵĴ��߽��ڵ�E�� 
��1����֤��CE�ǰ�Բ�����ߣ�
��2����OB=5��BC=8����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON=30�㣬BΪOM��һ�㣬BA��ON��A���ı���ABCDΪ�����Σ�PΪ����BM��һ���㣬����CP����CP�Ƶ�C˳ʱ�뷽����ת90���CE������BE����AB=4����BE����СֵΪ �� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com