
【题目】某班决定购买一些笔记本和文具盒做奖品.已知需要的笔记本数量是文具盒数量的3倍,购买的总费用不低于220元,但不高于250元.
(1)商店内笔记本的售价4元/本,文具盒的售价为10元/个,设购买笔记本的数量为x,按照班级所定的费用,有几种购买方案?每种方案中笔记本和文具盒数量各为多少?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)经过还价,老板同意4元/本的笔记本可打八折,10元/个的文具盒可打七折,用(2)中的最少费用最多还可以多买多少笔记本和文具盒?
【答案】(1)有两种购买方案:方案一:笔记本30本,文具盒10个;方案二:笔记本33本,文具盒11个;
(2)方案一的总费用最少,最少费用为220元;
(3)用(2)中的最少费用最多还可以多买9本笔记本和3个文具盒.
【解析】
(1)设笔记本的数量为x,根据题意列出不等式方程组.x取整数.
(2)根据(1)可求出答案.
(3)设用(2)中的最少费用最多还可以多买的文具盒的数量为y,列出不等式求解,y取整数.
(1)设笔记本的数量为x本,根据题意得:
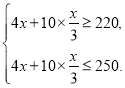
解得![]() .
.
∵x为正整数,
∴x可取30,31,32,33,34.
又∵![]() 也必须是整数,
也必须是整数,
∴![]() 可取10,11.
可取10,11.
∴有两种购买方案:
方案一:笔记本30本,文具盒10个;
方案二:笔记本33本,文具盒11个
(2)在(1)中,方案一购买的总数量最少,所以总费用最少.
最少费用为:4×30+10×10=220.
答:方案一的总费用最少,最少费用为220元.
(3)设用(2)中的最少费用最多还可以多买的文具盒数量为y,则笔记本数量为3y,
由题意得 4×80%(30+3y)+10×70%(10+y)≤220,
解得:![]() ,
,
∵y为正整数,
∴满足![]() 的最大正整数为3.
的最大正整数为3.
∴多买的笔记本为:3y=9(本).
答:用(2)中的最少费用最多还可以多买9本笔记本和3个文具盒.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:

(1)A,B两城相距多少千米?
(2)分别求甲、乙两车离开A城的距离y与x的关系式.
(3)求乙车出发后几小时追上甲车?
(4)求甲车出发几小时的时候,甲、乙两车相距50千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
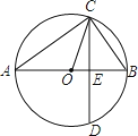
(1)求证:∠ACO=∠BCD;
(2)若BE=3,CD=8,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]()
(1)在平面直角坐标系内画出该函数的图象;
(2)当自变量x=-4时,函数y的值_________;
(3)当x<0时,请结合图象,直接写出y的取值范围:_______.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否>25?”为一次操作.
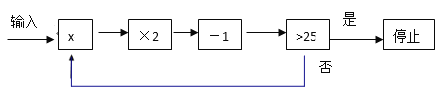
(1)如果操作只进行一次就停止,求x的取值范围;
(2)如果操作进行了四次才停止,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程
例:若代数式![]() 的值是
的值是![]() ,求
,求![]() 的取值范围.
的取值范围.
解:原式=![]()
当![]() 时,原式
时,原式![]() ,解得
,解得![]() (舍去);
(舍去);
当![]() 时,原式
时,原式![]() ,符合条件;
,符合条件;
当![]() 时,原式
时,原式![]() ,解得
,解得 ![]() (舍去).
(舍去).
所以,![]() 的取值范围是
的取值范围是![]()
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
![]() 当
当![]() 时,化简:
时,化简:![]()
![]() 若等式
若等式![]() 成立,则
成立,则![]() 的取值范围是
的取值范围是
![]() 若
若![]() ,求
,求![]() 的取值.
的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
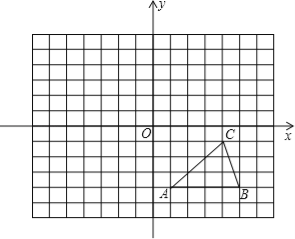
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com