
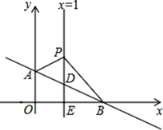
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌжБЯпAB:y= -![]() +bНЛyжсгкЕуA(0,1),НЛxжсгкЕуB,жБЯпx=1НЛABгкЕуD,НЛxжсгкЕуE,PЪЧжБЯпx=1ЩЯЕФвЛЖЏЕуЃЌЧвдкЕуDЕФЩЯЗНЃЌЩшP(1,n).
+bНЛyжсгкЕуA(0,1),НЛxжсгкЕуB,жБЯпx=1НЛABгкЕуD,НЛxжсгкЕуE,PЪЧжБЯпx=1ЩЯЕФвЛЖЏЕуЃЌЧвдкЕуDЕФЩЯЗНЃЌЩшP(1,n).
(1)ЧѓжБЯпABdНтЮіЪНКЭЕуBЕФзјБъЃЛ
(2)ЧѓЁїABPЕФУцЛ§(гУКЌnЕФДњЪ§ЪНБэЪО)ЃЛ
(3) ЕБ![]() =2ЪБ,
=2ЪБ,
ЂйЧѓГіЕуPЕФзјБъЃЛЂкдкЂйЕФЬѕМўЯТЃЌвдPBЮЊБпдкЕквЛЯѓЯозїЕШбќжБНЧЁїBPCЃЌжБНгаДГіЕуCЕФзјБъЃЎ
ЁОД№АИЁП(1) y=Ѓ![]() x+1, ЕуBЃЈ3ЃЌ0ЃЉ;(2)
x+1, ЕуBЃЈ3ЃЌ0ЃЉ;(2) ![]() nЃ1;(3)ЂйP(1ЃЌ2)ЃЛЂкЃЈ3ЃЌ4ЃЉЛђЃЈ5ЃЌ2ЃЉЛђЃЈ3ЃЌ2ЃЉ.
nЃ1;(3)ЂйP(1ЃЌ2)ЃЛЂкЃЈ3ЃЌ4ЃЉЛђЃЈ5ЃЌ2ЃЉЛђЃЈ3ЃЌ2ЃЉ.
ЁОНтЮіЁП
(1)НЋЕуAЕФзјБъДњШыжБЯпABЕФНтЮіЪНПЩЧѓЕУbжЕЃЌПЩЕУABЕФНтЮіЪНЃЌМЬЖјСюy=0ЃЌЧѓЕУЯргІЕФxжЕМДПЩЕУЕуЮЊBЕФзјБъЃЛ
(2)Й§ЕуAзїAMЁЭPDЃЌДЙзуЮЊMЃЌЧѓЕУAMЕФГЄЃЌдйЧѓЕУЁїBPDКЭЁїPADЕФУцЛ§ЃЌЖўепЕФКЭМДЮЊЁїABPЕФУцЛ§ЃЛ
(3)ЂйЕБSЁїABP=2ЪБЃЌДњШыЂйжаЫљЕУЕФДњЪ§ЪНЃЌЧѓЕУnжЕЃЌМДПЩЧѓЕУЕуPЕФзјБъЃЛ
ЂкЗжPЪЧжБНЧЖЅЕуЧвBP=PCЁЂBЪЧжБНЧЖЅЕуЧвBP=BC ЁЂCЪЧжБНЧЖЅЕуЧвCP=CBШ§жжЧщПіЧѓЕуCЕФзјБъМДПЩЃЎ
(1)Ёпy=Ѓ![]() x+bОЙ§A(0ЃЌ1)ЃЌЁрb=1ЃЌ
x+bОЙ§A(0ЃЌ1)ЃЌЁрb=1ЃЌ
ЁржБЯпABЕФНтЮіЪНЪЧy=Ѓ![]() x+1ЃЌ
x+1ЃЌ
ЕБy=0ЪБЃЌ0=Ѓ![]() x+1ЃЌНтЕУx=3ЃЌЁрЕуB(3ЃЌ0)ЃЛ
x+1ЃЌНтЕУx=3ЃЌЁрЕуB(3ЃЌ0)ЃЛ
(2)Й§ЕуAзїAMЁЭPDЃЌДЙзуЮЊMЃЌдђгаAM=1ЃЌ

Ёпx=1ЪБЃЌy=Ѓ![]() x+1=
x+1=![]() ЃЌ PдкЕуDЕФЩЯЗНЃЌЁрPD=nЃ
ЃЌ PдкЕуDЕФЩЯЗНЃЌЁрPD=nЃ![]() ЃЌ
ЃЌ
SЁїAPD=![]() PDAM=
PDAM=![]() ЁС1ЁС(nЃ
ЁС1ЁС(nЃ![]() )=
)=![]() nЃ
nЃ![]() ЃЌ
ЃЌ
гЩЕуB(3ЃЌ0)ЃЌПЩжЊЕуBЕНжБЯпx=1ЕФОрРыЮЊ2ЃЌ
МДЁїBDPЕФБпPDЩЯЕФИпГЄЮЊ2ЃЌ
ЁрSЁїBPD=![]() PDЁС2=nЃ
PDЁС2=nЃ![]() ЃЌ
ЃЌ
ЁрSЁїPAB=SЁїAPD+SЁїBPD=![]() nЃ
nЃ![]() +nЃ
+nЃ![]() =
=![]() nЃ1ЃЛ
nЃ1ЃЛ
(3)ЂйЕБSЁїABP=2ЪБЃЌ![]() nЃ1=2ЃЌНтЕУn=2ЃЌЁрЕуP(1ЃЌ2)ЃЛ
nЃ1=2ЃЌНтЕУn=2ЃЌЁрЕуP(1ЃЌ2)ЃЛ
ЂкЁпE(1ЃЌ0)ЃЌ
ЁрPE=BE=2ЃЌ
ЁрЁЯEPB=ЁЯEBP=45ЁуЃЎ
Ек1жжЧщПіЃЌШчЭМ1ЃЌЁЯCPB=90ЁуЃЌBP=PCЃЌ
Й§ЕуCзїCNЁЭжБЯпx=1гкЕуNЃЎ

ЁпЁЯCPB=90ЁуЃЌЁЯEPB=45ЁуЃЌ
ЁрЁЯNPC=ЁЯEPB=45ЁуЃЌ
дкЁїCNPгыЁїBEPжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїCNPЁеЁїBEPЃЌ
ЁрPN=NC=EB=PE=2ЃЌ
ЁрNE=NP+PE=2+2=4ЃЌ
ЁрC(3ЃЌ4)ЃЛ
Ек2жжЧщПіЃЌШчЭМ2ЃЌЁЯPBC=90ЁуЃЌBP=BCЃЌ
Й§ЕуCзїCFЁЭxжсгкЕуFЃЎ

ЁпЁЯPBC=90ЁуЃЌЁЯEBP=45ЁуЃЌ
ЁрЁЯCBF=ЁЯPBE=45ЁуЃЌ
дкЁїCBPгыЁїPBEжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїCBFЁеЁїPBEЃЎ
ЁрBF=CF=PE=EB=2ЃЌ
ЁрOF=OB+BF=3+2=5ЃЌ
ЁрC(5ЃЌ2)ЃЛ
Ек3жжЧщПіЃЌШчЭМ3ЃЌЁЯPCB=90ЁуЃЌCP=CBЃЌ
ЁрЁЯCPB=ЁЯCBP=45ЁуЃЌ

ЁпЁЯEPB=ЁЯEBP=45ЁуЃЌ
ЁрЁЯPCB=ЁЯCBE=ЁЯEPC=90ЁуЃЌ
ЁрЫФБпаЮEBCPЮЊОиаЮЃЌ
ЁпCP=CBЃЌ
ЁрЫФБпаЮEBCPЮЊе§ЗНаЮЃЌ
ЁрPC=CB=PE=EB=2ЃЌ
ЁрC(3ЃЌ2)ЃЛ
ЁрвдPBЮЊБпдкЕквЛЯѓЯозїЕШбќжБНЧШ§НЧаЮBPCЃЌЕуCЕФзјБъЪЧ(3ЃЌ4)Лђ(5ЃЌ2)Лђ(3ЃЌ2)ЃЎ


 ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
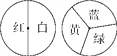
ЁОЬтФПЁПаЁУїКЭаЁССгУШчЭМЫљЪОЕФСНИізЊХЬзіЁАХфзЯЩЋЁБгЮЯЗЃЌгЮЯЗЙцдђЪЧЃКЗжБ№зЊЖЏСНИізЊХЬЃЌШєЦфжавЛИізЊХЬзЊГіКьЩЋЃЌСэвЛИізЊГіРЖЩЋЃЌдђПЩвдХфГЩзЯЩЋЃЌДЫЪБаЁУїЕУ1ЗжЃЌЗёдђаЁССЕУ1ЗжЃЎ
(1)гУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіаЁУїЛёЪЄЕФИХТЪЃЛ
(2)етИігЮЯЗЖдЫЋЗНЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЎШєВЛЙЋЦНЃЌШчКЮаоИФЙцдђВХФмЪЙгЮЯЗЖдЫЋЗНЙЋЦНЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаРэЪ§aЁЂbЁЂcдкЪ§жсЩЯЖдгІЕуЕФЮЛжУШчЭМЃКЂй abcЃМ0ЃЛЂк (aЃb)(bЃc)(cЃa)ЃО0ЃЛЂл|a|ЃМ1ЃbcЃЛЂм|aЃb|ЃЋ|bЃc|ЃН|aЃc|ЃЛвдЩЯЫФИіНсТле§ШЗЕФгаЃЈ ЃЉИі.
![]()
A.4B.3C.2D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЮЊШёНЧШ§НЧаЮЃЌADЪЧBCБпЩЯЕФИпЃЌе§ЗНаЮEFGHЕФвЛБпFGдкBCЩЯЃЌЖЅЕуEЁЂHЗжБ№дкABЁЂACЩЯЃЌвбжЊBC=40cmЃЌAD=30cmЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAEHЁзЁїABCЃЛ
ЃЈ2ЃЉЧѓетИіе§ЗНаЮЕФБпГЄгыУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙЩУёЭѕЯўгюЩЯжмЮхдкЙЩЪавдЪеХЬМлЃЈЙЩЪаЪеЪаЪБЕФМлИёЃЉУПЙЩ24дЊЙКТђНјФГЙЋЫОЙЩЦБ1000ЙЩЃЌжмСљЁЂжмШеЙЩЪаВЛНЛвзЃЌдкНгЯТРДЕФвЛжмНЛвзШеФкЃЌЭѕЯўгюМЧЯТИУЙЩУПШеЪеХЬМлИёЯрБШЧАвЛЬьЕФеЧЕјЧщПіШчЯТБэЃКЃЈЕЅЮЛЃКдЊЃЉ

ЃЈ1ЃЉаЧЦкШ§ЪеХЬЪБЃЌУПЙЩЪЧЖрЩйдЊЃП
ЃЈ2ЃЉвбжЊаЁУїИИЧзТђНјЙЩЦБЪБИЖСЫ1.5ЁыЕФЪжајЗбЃЌТєГіЪБашИЖГЩНЛЖюЕФ1.5ЁыЕФЪжајЗбКЭ1ЁыЕФНЛвзЫАЃЌШчЙћЫћдкжмЮхЪеХЬЧАНЋШЋВПЙЩЦБТєГіЃЌЫћЕФЪевцЧщПіШчКЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМЂйЪЧвЛИіШ§НЧаЮЃЌЗжБ№СЌНгетИіШ§НЧаЮШ§БпЕФжаЕуЕУЕНЭМЂкЃЌдйЗжБ№СЌНгЭМЂкжаМфаЁШ§НЧаЮШ§БпЕФжаЕуЃЌЕУЕНЭМЂл.

(1)ЭМЂкга______ИіШ§НЧаЮЃЛЭМЂлга______ИіШ§НЧаЮЃЛ
(2)АДЩЯУцЕФЗНЗЈМЬајЯТШЅЃЌЕкnИіЭМаЮжага_________ИіШ§НЧаЮ(гУnЕФДњЪ§ЪНБэЪО).
(3)ЪЧЗёДцдке§ећЪ§nЃЌЪЙЕУЕкnИіЭМаЮжаДцдк2019ИіШ§НЧаЮ?ШчЙћДцдкЃЌЧыЧѓГіnЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
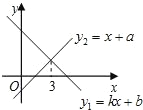
ЁОЬтФПЁПвЛДЮКЏЪ§ y1ЃНkx+b гы y2ЃНx+a ЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйkЃМ0ЃЛЂкaЃМ0ЃЌbЃМ0ЃЛЂлЕБ xЃН3 ЪБЃЌy1ЃНy2ЃЛЂмВЛЕШЪН kx+bЃОx+a ЕФНтМЏЪЧ xЃМ3ЃЌЦфжае§ШЗЕФНсТлга_______ЃЎЃЈжЛЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГѕЖўФъМЖНЬЪІЖдЪдОэНВЦРПЮжабЇЩњВЮгыЕФЩюЖШгыЙуЖШНјааЦРМлЕїВщЃЌЦфЦРМлЯюФПЮЊжїЖЏжЪвЩЁЂЖРСЂЫМПМЁЂзЈзЂЬ§НВЁЂНВНтЬтФПЫФЯюЃЎЦРМлзщЫцЛњГщШЁСЫШєИЩУћГѕЖўбЇЩњЕФВЮгыЧщПіЃЌЛцжЦГЩШчЭМЫљЪОЕФЦЕЪ§ЗжВМжБЗНЭМКЭЩШаЮЭГМЦЭМЃЈОљВЛЭъећЃЉЃЌЧыИљОнЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉдкетДЮЦРМлжаЃЌвЛЙВГщВщСЫ УћбЇЩњЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЯюФПЁАжїЖЏжЪвЩЁБЫљдкЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ ЖШЃЛ
ЃЈ3ЃЉЧыНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ4ЃЉШчЙћШЋЪага6000УћГѕЖўбЇЩњЃЌФЧУДдкЪдОэЦРНВПЮжаЃЌЁАЖРСЂЫМПМЁБЕФГѕЖўбЇЩњдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпl1ЕФКЏЪ§НтЮіЪНЮЊy=Љ2x+4ЃЌЧвl1гыxжсНЛгкЕуDЃЌжБЯпl2ОЙ§ЕуAЁЂBЃЌжБЯпl1ЁЂl2НЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓжБЯпl2ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїADCЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкжБЯпl2ЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїADPУцЛ§ЪЧЁїADCУцЛ§ЕФ2БЖЃПШчЙћДцдкЃЌЧыЧѓГіPзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com