
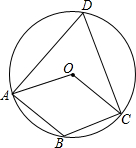
 如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°.
如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°. 分析 利用四边形OABC为平行四边形,可得∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.利用四边形ABCD是圆的内接四边形,可得∠D+∠B=180°.利用同弧所对的圆周角和圆心角可得∠D=$\frac{1}{2}$∠AOC,求出∠D=60°,进而即可得出.
解答 解:∵四边形OABC为平行四边形,
∴∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.
∵四边形ABCD是圆的内接四边形,
∴∠D+∠B=180°.
又∠D=$\frac{1}{2}$∠AOC,
∴3∠D=180°,
解得∠D=60°.
∴∠OAB=∠OCB=180°-∠B=60°.
∴∠OAD+∠OCD=360°-(∠D+∠B+∠OAB+∠OCB)=360°-(60°+120°+60°+60°)=60°.
故答案为:60.
点评 本题考查了平行四边形的性质、圆的内接四边形的性质、同弧所对的圆周角和圆心角的关系,属于基础题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
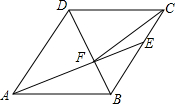 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为12$\sqrt{3}$,其中一定成立的是①②③(把所有正确结论的序号都填在横线上)①②③.
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为12$\sqrt{3}$,其中一定成立的是①②③(把所有正确结论的序号都填在横线上)①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
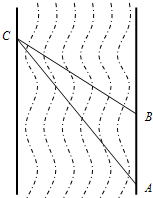 小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.
小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
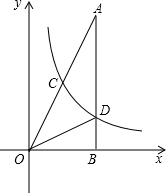 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4,则点C的坐标为(2,4).
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4,则点C的坐标为(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com