
【题目】已知二次函数![]() .
.
(1)若此函数图象与![]() 轴只有一个交点,试写出
轴只有一个交点,试写出![]() 与
与![]() 满足的关系式.
满足的关系式.
(2)若![]() ,点
,点![]() ,
,![]() ,
,![]() 是该函数图象上的3个点,试比较
是该函数图象上的3个点,试比较![]() ,
,![]() ,
,![]() 的大小.
的大小.
(3)若![]() ,当
,当![]() 时,函数
时,函数![]() 随
随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)
;(3)![]()
【解析】
(1)根据![]() 即可求解;
即可求解;
(2)当![]() 时,二次函数图象的对称轴为
时,二次函数图象的对称轴为![]() ,即
,即![]() 为顶点.再分a<0和a>0两种情况分别讨论解决;
为顶点.再分a<0和a>0两种情况分别讨论解决;
(3)当![]() 时,即函数表达式为
时,即函数表达式为![]() ,得出函数图象经过定点
,得出函数图象经过定点![]() ,
,![]() .要当
.要当![]() 时,函数
时,函数![]() 随
随![]() 的增大而增大. 必须满足:图象开口向上,对称轴在直线
的增大而增大. 必须满足:图象开口向上,对称轴在直线![]() 的左侧,即可解题.
的左侧,即可解题.
解:(1)由条件得,![]() ,即
,即![]() .
.
(2)当![]() 时,二次函数图象的对称轴为
时,二次函数图象的对称轴为![]() ,即
,即![]() 为顶点.
为顶点.
①当![]() 时,图象开口向上,
时,图象开口向上,![]() 为最小值,
为最小值,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②当![]() 时,图象开口向下,
时,图象开口向下,![]() 为最大值,
为最大值,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
(3)当![]() 时,即函数表达式为
时,即函数表达式为![]() ,
,
∴函数图象经过定点![]() ,
,![]() .
.
∴要当![]() 时,函数
时,函数![]() 随
随![]() 的增大而增大.
的增大而增大.
必须满足:图象开口向上,对称轴在直线![]() 的左侧,
的左侧,
即![]() ,
,![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,点O在线段AB上,AO=4,OB=2,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做运动,设运动时间为t秒.

(1)当t=1秒时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.为了求AQBP的值,小华同学尝试过O点作OE∥AP交BP于点E,试利用小华同学给我们的启发补全图形并求AQBP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
![]()
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①②B. ①③C. ①②③D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3)、B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
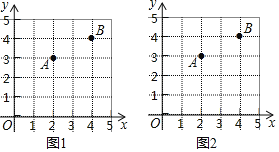
(1)在图1中画一个△QAB,使点Q的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P、B横坐标的平方和等于它们纵坐标和的4倍;
(3)在图2中的线段AB上确定点N,连结线段PN,使S△PAN=S△PBN.
查看答案和解析>>
科目:初中数学 来源: 题型:
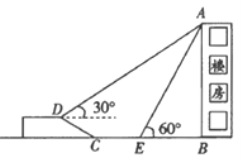
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为300 ,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为600 .已知坡面CD=10米,山坡的坡度![]() (坡度 是指坡面的铅直高度与水平宽度的比),
(坡度 是指坡面的铅直高度与水平宽度的比),
(1)求点D离地面高度(即点D到直线BC的距离);
(2)求楼房AB高度.(结果保留根式)
查看答案和解析>>
科目:初中数学 来源: 题型:
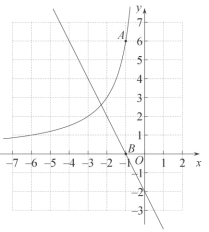
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.
(1)求抛物线的函数解析式以及顶点D的坐标;
(2)在抛物线上取一点P(不与点C重合)、并分别连接PA、PD,当△PAD的面积与△ACD的面积相等时,求点P的坐标:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com