
 如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且 CE=CF.连接CA、CD、CB.
如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且 CE=CF.连接CA、CD、CB.分析 (1)连接OC,可先证明AC平分∠BAE,结合圆的性质可证明OC∥AE,可得∠OCB=90°,可证得结论;
(2)可先证得四边形AOCD为平行四边形,再证明△OCB为等边三角形,可求得CF、AB,利用梯形的面积公式可求得答案.
解答  (1)证明:如图,连结OC.
(1)证明:如图,连结OC.
∵CF⊥AB,CE⊥AD,且CE=CF,
∴∠CAE=∠CAB,
∵OC=OA,
∴∠CAB=∠OCA,
∴∠CAE=∠OCA,
∴OC∥AE,
∴∠AEC+∠OCE=90°,
∴∠OCE=90°,即OC⊥CE,
∵OC是⊙O的半径,点C为半径外端,
∴CE是⊙O的切线;
(2)解:∵AD=CD,
∴∠DAC=∠DCA=∠CAB,
∴DC∥AB,
∵∠CAE=∠OCA,
∴OC∥AD,
∴四边形AOCD是平行四边形,
∴OC=AD=6,AB=12,
∵∠CAE=∠CAB,
∴CD=CB=6,
∴CB=OC=OB,
∴△OCB是等边三角形,
在Rt△CFB中,CF=$\sqrt{C{B}^{2}-F{B}^{2}}$=3$\sqrt{3}$,
∴S四边形ABCD=$\frac{1}{2}$(DC+AB)•CF=$\frac{1}{2}$×(6+12)×3$\sqrt{3}$=27$\sqrt{3}$.
点评 本题主要考查切线的判定,掌握切线的两种判定方法是解题的关键,即有切点时连接圆心和切点,然后证明垂直,没有切点时,过圆心作垂直,证明圆心到直线的距离等于半径.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:选择题
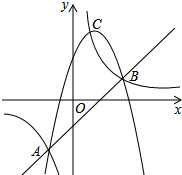 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论:
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
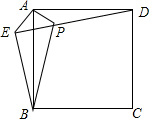 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小林同学利用暑假参观了幸福村果树种植基地(如图),他出发沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(5,-3),(5,0),(5,4)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点.
小林同学利用暑假参观了幸福村果树种植基地(如图),他出发沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(5,-3),(5,0),(5,4)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的直径垂直于弦 | |
| B. | 把(a-2)$\sqrt{\frac{1}{2-a}}$根号外的因式移到根号内后,其结果是-$\sqrt{2-a}$ | |
| C. | 相等的圆心角所对的弧相等 | |
| D. | 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com