
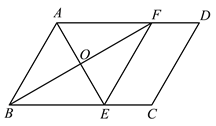
【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.
【答案】(1)证明见解析(2)2![]()
【解析】分析:(1)利用两对边分另相等的四边形是平行四边形,再根据邻边相等的平行四边形是菱形即可证明;
(2)过点A作AG⊥BC于点G,利用等边三角形的性质、矩形的判定,含30度角的直角三角形即可求出CF的长.
详解:(1)证明:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵□ABCD,
∴AD∥B,
∴∠AFB=∠CBF,
∴∠ABF=∠AFB,
∴AB=AF,
∵AE⊥BF,
∴∠ABF+∠BAO=∠CBF+∠BEO=90°,
∴∠BAO=∠BEO,
∴AB=BE,
∴AF=BE,
∴四边形ABEF是平行四边形,
∴□ABEF是菱形.
(2)解:∵AD=BC,AF=BE,
∴DF=CE,
∴BE=2CE,
∵AB=4,
∴BE=4,
∴CE=2,
过点A作AG⊥BC于点G,
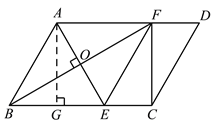
∵∠ABC=60°,AB=BE,
∴△ABE是等边三角形,
∴BG=GE=2,
∴AF=CG=4,
∴四边形AGCF是平行四边形,
∴□AGCF是矩形,
∴AG=CF,
在△ABG中,∠ABC=60°,AB=4,
∴AG=![]() ,
,
∴CF=![]() ,
,


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
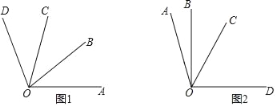
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
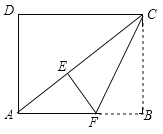
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出![]() ,并直接写出线段DH的长.
,并直接写出线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
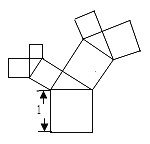
A.1B.2018C.2019D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
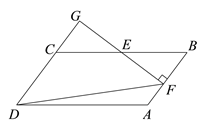
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标号1、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜。否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上![]() 两点相距
两点相距![]() 个单位长度,机器人从
个单位长度,机器人从![]() 点出发去
点出发去![]() 点,
点,![]() 点在
点在![]() 点右侧.规定向右为前进,第一次它前进
点右侧.规定向右为前进,第一次它前进![]() 个单位长度,第二次它后退
个单位长度,第二次它后退![]() 个单位长度,第三次再前进
个单位长度,第三次再前进![]() 个单位长度,第四次又后退
个单位长度,第四次又后退![]() 个单位长度……按此规律行进,如果
个单位长度……按此规律行进,如果![]() 点在数轴上表示的数为
点在数轴上表示的数为![]() ,那么
,那么
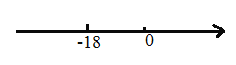
(1)求出![]() 点在数轴上表示的数.
点在数轴上表示的数.
(2)经过第七次行进后机器人到达点![]() ,第八次行进后到达点
,第八次行进后到达点![]() ,点
,点![]() 到
到![]() 点的距离相等吗?请说明理由.
点的距离相等吗?请说明理由.
(3)机器人在未到达![]() 点之前,经过
点之前,经过![]() 次(
次(![]() 为正整数)行进后,它在数轴上表示的数应如何用含
为正整数)行进后,它在数轴上表示的数应如何用含![]() 的代数式表示?
的代数式表示?
(4)如果![]() 点在原点的右侧,那么机器人经过
点在原点的右侧,那么机器人经过![]() 次行进后,它在
次行进后,它在![]() 点的什么位置?请通过计算说明.
点的什么位置?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22018+22019,①将等式两边同时乘2,得
2S=2+22+23+24+25+…+22019+22020,②
将②式减去①式,得2S-S=22020-1,
即S=22020-1,
则1+2+22+23+24+…+22019=22020-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+210;
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com