
【题目】在平行四边形ABCD中E是BC边上一点,且AB=AE,AE,DC的延长线相交于点F.

(1)若∠F=62°,求∠D的度数;
(2)若BE=3EC,且△EFC的面积为1,求平行四边形ABCD的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由四边形ABCD是平行四边形,∠F=62°,易求得∠BAE的度数,又由AB=BE,即可求得∠B的度数,然后由平形四边形的对角相等,即可求得∠D的度数;
(2)根据相似三角形的性质求出△FEC与△FAD的相似比,得到其面积比,再找到△FEC与平行四边形的关系,求出平行四边形的面积.
(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAF=∠F=62°,
∵AB=BE,
∴∠AEB=∠BAE=62°,
∴∠B=180°-∠BAE-∠AEB=56°,
∵在平行四边形ABCD中,∠D=∠B,
∴∠D=56°.
(2)∵DC∥AB,
∴△CEF∽△BEA.
∵BE=3EC
∴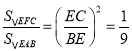 ,
,
∵S△EFC=1.
∴S△ABE=9a,
∵![]()
∴![]()
∴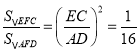
∴![]()
∵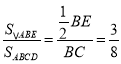
∴![]()


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 出发在一条直线上来回爬行,规定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次记为(单位:
出发在一条直线上来回爬行,规定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次记为(单位:![]() )-11、+8、+9、-3、-6、+12、-9.
)-11、+8、+9、-3、-6、+12、-9.
(1)小虫最后中否回到出发点,请判断并且通过计算说明理由.
(2)在爬行的过程中,如果每爬行一个单位长度奖励一粒芝麻,则整个运动过程中小虫一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为![]() ,
,![]() ,
,![]() ,
,![]() , ……,则
, ……,则![]() 的坐标为________________.
的坐标为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,过点A作
,过点A作![]() 轴于点B,连结
轴于点B,连结![]() .
.
(1)求k的值;
(2)如图,若直线![]() 经过点A,与x轴相交于点C,且满足
经过点A,与x轴相交于点C,且满足![]() .求:
.求:
①直线![]() 的表达式;
的表达式;
②记直线![]() 与双曲线
与双曲线![]() 的另一交点为
的另一交点为![]() ,试求
,试求![]() 的面积
的面积![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=![]() .tanD=tan15°=
.tanD=tan15°=![]() =
= =
=![]() .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=![]() .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=![]() =
=![]() =
=![]() .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,矩形ABCD的顶点A、B分别在OM、ON上,当B在边ON上运动时,A 随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,则运动过程中,点C到点O的最大距离为___________.
,矩形ABCD的顶点A、B分别在OM、ON上,当B在边ON上运动时,A 随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,则运动过程中,点C到点O的最大距离为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,9,3分)正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )

A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com