Question

1．如图，在⊙O中，BC为⊙O的弦，点A在半径OD上，连接AB、AC，$\widehat{BD}$=$\widehat{CD}$．
（1）如图1，求证：△ABC是等腰三角形；
（2）如图2，延长DO交BC于F，延长BO交AC于G，交⊙O于E，若AO=2OF，求证：点G为AC的中点；
（3）如图3在（2）的条件下，连接CE，H在FC上，直线GH交⊙O于M、N，若CA平分∠BCE，OF=FH，BC=6，求MN的长．

Answer 1

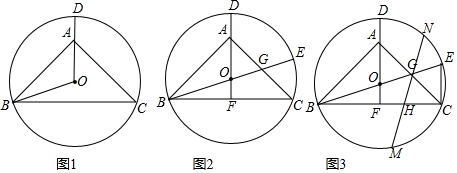
分析 （1）如图1中，延长DO交BC于F．根据垂径定理可得DF垂直平分BC，由此可得AB=AC．
（2）如图2中，连接EC，AE，OC，只要证明四边形AOCE是平行四边形即可解决问题．
（3）如图3中，连接OC交MN于K，连接OM．首先证明OC⊥MN，求出OK、OM即可解决问题．

解答 （1）证明：如图1中，延长DO交BC于F．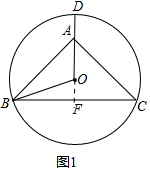

∵$\widehat{BD}$=$\widehat{CD}$，
∴DF⊥BC，
∴BF=CF，
∴AB=AC，
∴△ABC是等腰三角形．

（2）证明：如图2中，连接EC，AE，OC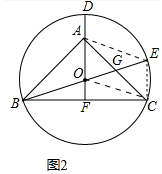

∵BO=OE，BF=FC，
∴OF∥EC，EC=2OF，
∵AO=2OF，
∴OA=EC，∵OA∥EC，
∴四边形AOCE是平行四边形，
∴AG=CG，即G是AC中点．

（3）解：如图3中，连接OC交MN于K，连接OM．

∵AC平分∠BCE，∠BCE=90°，
∴∠ECA=∠ACB=∠ABC=45°，
∴∠BAC=90°，
∵BC=6，
∴AF=BF=CF=3，OA=2，OF=FH=1，HC=EC=2，
∵CG=CG，∠GCH=∠GCE，CH=CE，
∴△CGH≌△CGE，
∴∠∠CHG=∠CEG，
∵∠CBE+∠CEG=90°，
∵OB=OC，
∴∠CBE=∠OCB，
∴∠OCB+∠CHG=90°，
∴∠CKH=90°，
∴OK⊥MN，MK=KN，
∵△CKH∽△CFO，
∴$\frac{CK}{CF}$=$\frac{CH}{CO}$，∵OC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
∴$\frac{CK}{3}$=$\frac{2}{\sqrt{10}}$，
∴CK=$\frac{3}{5}$$\sqrt{10}$，
∴OK=OC-CK=$\frac{2}{5}$$\sqrt{10}$，
∴MK=$\sqrt{O{M}^{2}-O{K}^{2}}$=$\sqrt{10-\frac{40}{25}}$=$\frac{\sqrt{210}}{5}$，
∴MN=2MK=$\frac{2\sqrt{210}}{5}$．

点评 本题考查圆综合题、垂径定理、全等三角形的判定和性质．相似三角形的判定和性质、勾股定理等知识，综合性比较强，解题的关键是灵活运用所学知识，学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．