
分析 (1)根据完全平方公式、单项式乘多项式可以解答本题;
(2)根据分式的减法和除法可以解答本题.
解答 解:(1)(a-2b)2-a(a-4b)
=a2-4ab+4b2-a2+4ab
=4b2;
(2)($\frac{8-4x}{x+2}$-2+x)÷$\frac{{x}^{2}-2x}{x+2}$
=$\frac{8-4x-(2-x)(x+2)}{x+2}•\frac{x+2}{x(x-2)}$
=$\frac{8-4x-4+{x}^{2}}{x(x-2)}$
=$\frac{(x-2)^{2}}{x(x-2)}$
=$\frac{x-2}{x}$.
点评 本题考查分式的混合运算、单项式乘多项式、完全平方公式,解答本题的关键是明确它们各自的计算方法.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
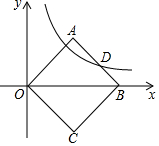 如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.
如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com