
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
【答案】![]() ;2或﹣1
;2或﹣1
【解析】解:min{﹣ ![]() ,﹣
,﹣ ![]() }=﹣
}=﹣ ![]() , ∵min{(x﹣1)2 , x2}=1,
, ∵min{(x﹣1)2 , x2}=1,
∴当x>0.5时,(x﹣1)2=1,
x﹣1=±1,
x﹣1=1,x﹣1=﹣1,
解得:x1=2,x2=0(不合题意,舍去),
当x≤0.5时,x2=1,
解得:x1=1(不合题意,舍去),x2=﹣1,
所以答案是: ![]() ;2或﹣1.
;2或﹣1.
【考点精析】掌握二次函数的性质和实数的大小比较是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;数轴比较;求差比较;求商比较法;绝对值比较法;平方法.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 坐标分别是
坐标分别是![]() ,且
,且![]() 满足
满足![]() ,现同时将点
,现同时将点![]() 分别向下平移3个单位,再向左平移1个单位,分别得到点
分别向下平移3个单位,再向左平移1个单位,分别得到点![]() 的对应点
的对应点![]() ,连接
,连接![]() .
.
(1)求点![]() 的坐标及四边形
的坐标及四边形![]() 的面积
的面积![]() ;
;
(2)在y轴上是否存在一点![]() ,连接
,连接![]() ,使
,使![]() ?若存在这样的点,求出点M的坐标,若不存在,试说明理由.
?若存在这样的点,求出点M的坐标,若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
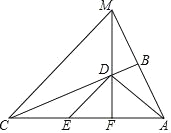
【题目】如图,∠ABC=90°,点D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB的延长线相交于点M,连接MC.
(1)MF与AC的位置关系是:______.
(2)求证:CF=MF.
(3)猜想:AD与MC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市“富美乡村建设”宣传活动,某社区对“推动富美乡村建设的政策与举措的了解情况”进行问卷调查,问卷中把了解情况分为“非常了解(A)”、“有些了解(B)”、“不了解(C)”三类,并将调查结果分析整理后,制成如图所示的两个统计图.
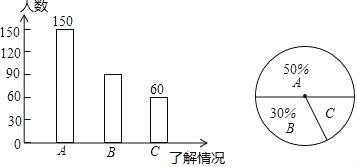
请根据以上两幅图的信息解答下列问题:
(1)这次调查活动共调查了_____人,其中“有些了解(B)”有_____人;
(2)在扇形统计图中,“B”所对应的扇形的圆心角度数是多少?
(3)如果该社区共有居民5000人,试估计“不了解(C)”的居民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法
解:∵x﹣y=2,∴x=y+2 又∵x>1∴y+2>1∴y>﹣1
又∵y<0∴﹣1<y<0…①
同理可得1<x<2…②
由①+②得:﹣1+1<x+y<0+2∴x+y的取值范围是0<x+y<2
按照上述方法,完成下列问题:
(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围是
(2)已知关于x,y的方程组![]() 的解都是正数
的解都是正数
①求a的取值范围;②若a﹣b=4,求a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com