
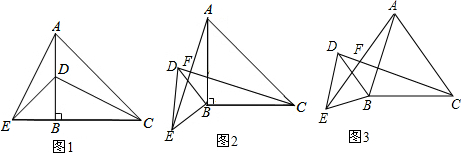
·ÖĪö Ąą±Č£ŗøł¾Ż”ĻDBE=”ĻABC=90”ć£¬µĆ³ö”ĻABE=”ĻDBC£¬ŌŁÖ¤³ö”÷AEB”Õ”÷CDB£¬AE=CD£¬”ĻEAB=”ĻDCB£¬ŌŁøł¾Ż”ĻDCB+”ĻCOB=90”ć£¬”ĻAOF=”ĻCOB£¬µĆ³ö”ĻFOA+”ĻFAO=90”ć£¬”ĻAFC=90”ć£¬¼“æÉÖ¤³öAE”ĶCD£»
ĶŲÕ¹£ŗ¢Łøł¾Ż”ĻDBE=”ĻABC=¦Į£¬ÓŚŹĒµĆµ½”ĻABE=”ĻDBC£¬ĶĘ³ö”÷AEB”Õ”÷CDB£¬¼“æɵƵ½½įĀŪ£»
¢ŚĶعż”÷AEB”Õ”÷CDB£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻEAB=”ĻDCB£¬ÓɶŌ¶„½ĒĻąµČµĆµ½”ĻAHF=”ĻCHB£¬ÓŚŹĒµĆµ½”ĻAFH=”ĻABC=¦Į£®
½ā“š ½ā£ŗĄą±Č£ŗAE=CD£¬AE”ĶCD£¬
Ö¤Ć÷£ŗ”ĻDBE=”ĻABC=90”ć£¬
”ą”ĻABE=”ĻDBC£¬
ŌŚ”÷AEBŗĶ”÷CDBÖŠ£¬
$\left\{\begin{array}{l}{AB=BC}\\{”ĻABE=”ĻDBC}\\{BE=BD}\end{array}\right.$£¬
”ą”÷AEB”Õ”÷CDB£¬
”ąAE=CD£¬”ĻEAB=”ĻDCB£¬
”ß”ĻDCB+”ĻCOB=90”ć£¬”ĻAOF=”ĻCOB£¬
”ą”ĻFOA+”ĻFAO=90”ć£¬
”ą”ĻAFC=90”ć£¬
”ąAE”ĶCD£»
ĶŲÕ¹£ŗ¢ŁAE=CD£¬
”ß”ĻDBE=”ĻABC=¦Į£¬
”ą”ĻABE=”ĻDBC£¬
ŌŚ”÷AEBŗĶ”÷CDBÖŠ£¬
$\left\{\begin{array}{l}{AB=BC}\\{”ĻABE=”ĻDBC}\\{BE=BD}\end{array}\right.$£¬
”ą”÷AEB”Õ”÷CDB£¬
”ąAE=CD£»
¢ŚĻ߶ĪAE£¬CDµÄĪ»ÖĆ¹ŲĻµ·¢Éśøı䣬ĘäĖłŌŚÖ±ĻߵļŠ½Ē“󊔲»Ėę×ÅĶ¼ŠĪµÄŠż×Ŗ¶ų·¢Éś±ä»Æ£¬
”ß”÷AEB”Õ”÷CDB£¬
”ą”ĻEAB=”ĻDCB£¬
”ß”ĻAHF=”ĻCHB£¬
”ą”ĻAFH=”ĻABC=¦Į£¬
”ąĻ߶ĪAE£¬CDµÄĪ»ÖĆ¹ŲĻµ·¢Éśøı䣬ĘäĖłŌŚÖ±ĻߵļŠ½Ē“󊔲»Ėę×ÅĶ¼ŠĪµÄŠż×Ŗ¶ų·¢Éś±ä»Æ£®Ź¼ÖÕĪŖ¦Į£®
µćĘĄ “ĖĢāæ¼²éĮĖČ«µČČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ”¢µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ”¢Šż×Ŗ±ä»»µČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒÄÜŌŚ½Ļø“ŌÓµÄĶ¼ŠĪÖŠÕŅ³öČ«µČµÄČż½ĒŠĪ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
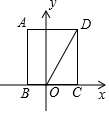 ČēĶ¼£¬¾ŲŠĪABCDµÄ±ßBCŌŚxÖįÉĻ£¬µćAŌŚµŚ¶žĻóĻŽ£¬µćDŌŚµŚŅ»ĻóĻŽ£¬AB=2$\sqrt{3}$£¬OD=4£¬½«¾ŲŠĪABCDČʵćOŠż×Ŗ£¬Ź¹µćDĀäŌŚxÖįÉĻ£¬ŌņµćC¶ŌÓ¦µćµÄ×ų±źŹĒ£Ø””””£©
ČēĶ¼£¬¾ŲŠĪABCDµÄ±ßBCŌŚxÖįÉĻ£¬µćAŌŚµŚ¶žĻóĻŽ£¬µćDŌŚµŚŅ»ĻóĻŽ£¬AB=2$\sqrt{3}$£¬OD=4£¬½«¾ŲŠĪABCDČʵćOŠż×Ŗ£¬Ź¹µćDĀäŌŚxÖįÉĻ£¬ŌņµćC¶ŌÓ¦µćµÄ×ų±źŹĒ£Ø””””£©| A£® | £Ø-$\sqrt{3}$£¬1£© | B£® | £Ø-1£¬$\sqrt{3}$£© | C£® | £Ø-1£¬$\sqrt{3}$£©»ņ£Ø1£¬-$\sqrt{3}$£© | D£® | £Ø-$\sqrt{3}$£¬1£©»ņ£Ø1£¬-$\sqrt{3}$£© |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 7 | B£® | 5 | C£® | 3 | D£® | 1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬ŅŌACĪŖÖ±¾¶µÄ”ŃO½»BCÓŚµćD£¬½»ABÓŚµćE£¬¹żµćD×÷DF”ĶAB£¬“¹×ćĪŖF£¬Į¬½ÓDE£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬ŅŌACĪŖÖ±¾¶µÄ”ŃO½»BCÓŚµćD£¬½»ABÓŚµćE£¬¹żµćD×÷DF”ĶAB£¬“¹×ćĪŖF£¬Į¬½ÓDE£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com