
【题目】阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是![]() 上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:
上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:![]() 是定值.
是定值.
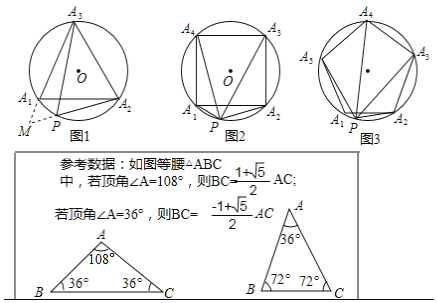
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
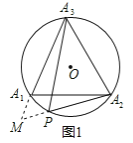
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问:![]() 还是定值吗?为什么?
还是定值吗?为什么?
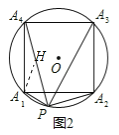
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则![]() = (只写出结果).
= (只写出结果).
【答案】(1)证明见解析;(2)是定值,理由见解析;(3)![]()
【解析】(2)结论:![]() 是定值.在A4P上截取AH=A2P,连接HA1.证明PA4=A4+PH=PA2+
是定值.在A4P上截取AH=A2P,连接HA1.证明PA4=A4+PH=PA2+![]() PA1,同法可证:PA3=PA1+
PA1,同法可证:PA3=PA1+![]() PA2,推出(
PA2,推出(![]() +1)(PA1+PA2)=PA3+PA4,可得PA1+PA2=(
+1)(PA1+PA2)=PA3+PA4,可得PA1+PA2=(![]() -1)(PA3+PA4),即可解决问题;
-1)(PA3+PA4),即可解决问题;
(3)结论:则![]() .如图3-1中,延长PA1到H,使得A1H=PA2,连接A4H,A4A2,A4A1.由△HA4A1≌△PA4A2,可得△A4HP是顶角为36°的等腰三角形,推出PH=
.如图3-1中,延长PA1到H,使得A1H=PA2,连接A4H,A4A2,A4A1.由△HA4A1≌△PA4A2,可得△A4HP是顶角为36°的等腰三角形,推出PH=![]() PA4,即PA1+PA2=
PA4,即PA1+PA2=![]() PA4,如图3-2中,延长PA5到H,使得A5H=PA3.同法可证:△A4HP是顶角为108°的等腰三角形,推出PH=
PA4,如图3-2中,延长PA5到H,使得A5H=PA3.同法可证:△A4HP是顶角为108°的等腰三角形,推出PH=![]() PA4,即PA5+PA3=
PA4,即PA5+PA3=![]() PA4,即可解决问题;
PA4,即可解决问题;
(1)如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M
∴PA3=MA2,
∵PM=PA1,
∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
(2)结论:![]() 是定值.
是定值.
理由:在A4P上截取AH=A2P,连接HA1.
∵四边形A1A2A3A4是正方形,
∴A4A1=A2A1,
∵∠A1A4H=∠A1A2P,A4H=A2P,
∴△A1A4H=△A1A2P,
∴A1H=PA1,∠A4A1H=∠A2A1P,
∴∠HA1P=∠A4A1A2=90°
∴△HA1P的等腰直角三角形,
∴PA4=HA4+PH=PA2+![]() PA1,
PA1,
同法可证:PA3=PA1+![]() PA2,
PA2,
∴(![]() +1)(PA1+PA2)=PA3+PA4,
+1)(PA1+PA2)=PA3+PA4,
∴PA1+PA2=(![]() -1)(PA3+PA4),
-1)(PA3+PA4),
∴![]() .
.
(3)结论:则![]() .
.
理由:如图3-1中,延长PA1到H,使得A1H=PA2,连接A4H,A4A2,A4A1.
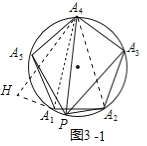
由△HA4A1≌△PA4A2,可得△A4HP是顶角为36°的等腰三角形,
∴PH=![]() PA4,即PA1+PA2=
PA4,即PA1+PA2=![]() PA4,
PA4,
如图3-2中,延长PA5到H,使得A5H=PA3.
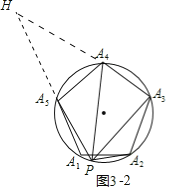
同法可证:△A4HP是顶角为108°的等腰三角形,
∴PH=![]() PA4,即PA5+PA3=
PA4,即PA5+PA3=![]() PA4,
PA4,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
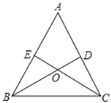
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某购物网店在双十一期间实行打折促销活动,规定如下表:
次性购物不大于100元不打折,不大于300元但大于100元打九折,超过300元的部分打八折.
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该网店一次性购物![]() 元,当
元,当![]() 低于300元但大于100元时,他实际付款多少元?当
低于300元但大于100元时,他实际付款多少元?当![]() 大于300元时,他实际付款多少元?(用含
大于300元时,他实际付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为![]() 元
元![]() ,用含
,用含![]() 的式子表示两次购物王老师实际付款多少元?
的式子表示两次购物王老师实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥DE,AB=DE,请你添加一个条件_______ 可以根据“ASA”使得△ABC≌△DEF;或者添加条件BE=CF,可以根据_______得到△ABC≌△DEF。
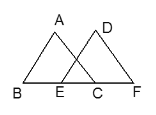
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
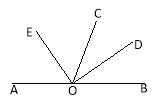
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
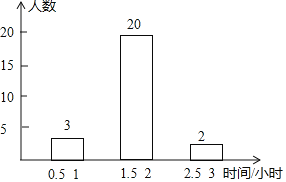
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级 | 做家务时间(小时) | 频数 | 百分比 |
A | 0.5≤x<1 | 3 | 6% |
B | 1<x<1.5 | a | 30% |
C | 1.5≤x<2 | 20 | 40% |
D | 2≤x<2.5 | b | m |
E | 2.5≤x<3 | 2 | 4% |
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
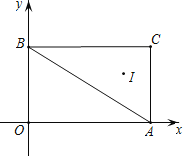
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com