
 ,OA=10cm,则AB长为 cm.
,OA=10cm,则AB长为 cm.
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:不详 题型:解答题
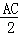 ,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.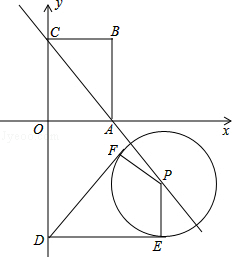
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 名称 | 四等分圆的面积 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
| 选用的工具 | 带刻度的三角板 | 量角器 | 带刻度的三角板、圆规 |
| 画出示意图 | 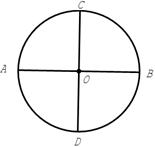 | | |
| 简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. | | |
| 指出对称性 | 既是轴对称图形又是中心对称图形 | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,AC=3
,AC=3 ,BC=6,则⊙O的半径是
,BC=6,则⊙O的半径是
 C.2
C.2 D.
D.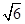
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com