Question

19．如图，已知抛物线y=-$\frac{1}{4}$x²+mx+n与x轴交于A （-2，0）、B两点，与y轴交于点C．抛物线对称轴为直线x=3，且对称轴与x轴交于点D．
（1）求抛物线的解析式；
（2）点P在线段BC上从点C开始向点B运动（点P不与点B、C重合），速度为每秒$\sqrt{5}$个单位，设运动时间为t（单位：s），过点P作x轴的垂线与抛物线相交于点F．求四边形CDBF的面积S关于t的函数关系式．

Answer 1

分析 （1）根据对称轴和点A的坐标，直接求出抛物线解析式；
（2）先确定出直线BC：y=-$\frac{1}{2}$x+4，设出点P坐标，表示出FP用面积的和，求出四边形CDBF的面积和点P的横坐标的关系，最后用相似三角形即可．

解答 （1）∵抛物线对称轴为直线x=3，
∴-$\frac{m}{{2×（-\frac{1}{4}）}}=3$，
∴m=$\frac{3}{2}$，
把A（-2，0）代入y=-$\frac{1}{4}$x²+$\frac{3}{2}$x+n中，得n=4，
∴抛物线的解析式为y=-$\frac{1}{4}$x²+$\frac{3}{2}$x+4，
（2）易得B（8，0），C（0，4）
设直线BC：y=kx+b，（k≠0）
∴$\left\{\begin{array}{l}{b=4}\\{8k+b=0}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$
∴直线BC：y=-$\frac{1}{2}$x+4，
设点P（p，-$\frac{1}{2}$p+4），
F（p，-$\frac{1}{4}$p²+$\frac{3}{2}$p+4），
∴$FP=-\frac{1}{4}{p^2}+\frac{3}{2}p+4-（{-\frac{1}{2}p+4}）=-\frac{1}{4}{p^2}+2p$，
∴S_{四边形CDBF}=S_△CDB+S_△CBF
=$\frac{1}{2}DB•OC+\frac{1}{2}FP•OB$
=$\frac{1}{2}×5×4+\frac{1}{2}×（{-\frac{1}{4}{p^2}+2p}）×8=-{p^2}+8p+10$，
在Rt△BCO中，BC=$\sqrt{C{O}^{2}+B{O}^{2}}$=4$\sqrt{5}$，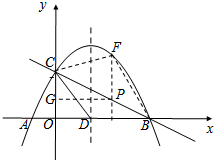


如图，过点P作PG⊥y轴于点G，
∴PG∥OB
∴△PCG∽△BCO，
∴$\frac{PC}{BC}=\frac{PG}{OB}$，
∴$\frac{\sqrt{5}t}{4\sqrt{5}}=\frac{p}{8}$，
∴p=2t
∴S_{四边形CDBF}=-4t²+16t+10．

点评 此题是二次函数综合题，主要考查了待定系数法，相似三角形的性质和判定，平面坐标系中几何图形面积的求法，解本题的关键是四边形CDBF的面积和点P的横坐标的关系．