
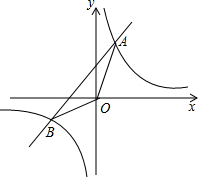
 如图,已知一次函数y=2x+3的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A,B两点,连接OA,OB,当△AOB的面积为$\frac{9}{2}$时,则k=$\frac{27}{8}$.
如图,已知一次函数y=2x+3的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A,B两点,连接OA,OB,当△AOB的面积为$\frac{9}{2}$时,则k=$\frac{27}{8}$. 分析 设A(m,2m+3),B(n,2n+3),直线AB交y轴于点C(0,3),思想利用三角形面积公式,求出m、n的关系,再根据A、B在y=$\frac{k}{x}$上,得到(n+3)(2n+9)=n(2n+3)=k,解方程即可.
解答 解:设A(m,2m+3),B(n,2n+3),直线AB交y轴于点C(0,3),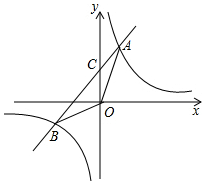
由题意:$\frac{1}{2}$×3(m-n)=$\frac{9}{2}$,
∴m-n=3,
∴m=n+3,
∴A(n+3,2n+9),
∵A、B在y=$\frac{k}{x}$上,
∴(n+3)(2n+9)=n(2n+3)=k,
∴n=-$\frac{9}{4}$,k=$\frac{27}{8}$,
故答案为$\frac{27}{8}$.
点评 本题考查一次函数与反比例函数的交点、三角形的面积公式,待定系数法等知识,解题的关键是灵活运用待定系数法,学会用方程的思想思考问题,属于中考填空题中的压轴题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
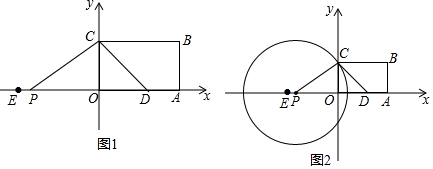
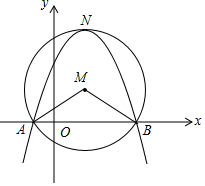 如图,在平面直角坐标系中,O是原点,以点M(2,2)为圆心,4为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点N在⊙M上.
如图,在平面直角坐标系中,O是原点,以点M(2,2)为圆心,4为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点N在⊙M上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
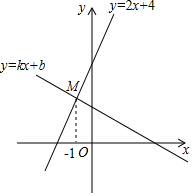 如图,已知直线y=2x+4与直线y=kx+b交于点M(-1,a),则关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y+4=0}\\{kx-y+b=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.
如图,已知直线y=2x+4与直线y=kx+b交于点M(-1,a),则关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y+4=0}\\{kx-y+b=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
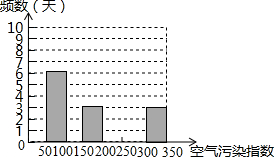 根据国家环保局统一规定,我国空气质量分为5个等级,当空气污染指数达到0-50时为1级;51-100时为2级,101-200时为3级;201-300时为4级;300以上时为5级,其中3级属于轻度污染,4级属于中度污染,5级属于重度污染.某城市环保局随机抽取了2013年某些天的空气质量检测数据,并整理绘制成如图频数分布表和频数分布直方图.
根据国家环保局统一规定,我国空气质量分为5个等级,当空气污染指数达到0-50时为1级;51-100时为2级,101-200时为3级;201-300时为4级;300以上时为5级,其中3级属于轻度污染,4级属于中度污染,5级属于重度污染.某城市环保局随机抽取了2013年某些天的空气质量检测数据,并整理绘制成如图频数分布表和频数分布直方图.| 空气污染指数 | 频数(天) | 频率 |
| 50<x≤100 | 6 | 0.2 |
| 100<x≤150 | a | 0.3 |
| 150<x≤200 | 3 | 0.1 |
| 200<x≤250 | 6 | 0.2 |
| 250<x≤300 | b | c |
| 300<x≤350 | 3 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com