练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．将方程2a-3b=6变形为用含a的式子表示b，那么b=$\frac{2}{3}a-2$．

    分析 把含b的项放到方程左边，移项，化系数为1，求b．

    解答 解：移项，得-3b=-2a+6，
    化系数为1，得b=$\frac{2}{3}$a-2，
    故答案为：$\frac{2}{3}a-2$．

    点评 本题考查的是方程的基本运算技能：移项、合并同类项、系数化为1等，关键是掌握表示谁就该把谁放到等号的一边，其他的项移到另一边，然后合并同类项、系数化1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

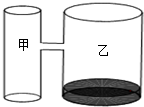    5．实验室里，水平桌面上有甲、乙两个圆柱形容器（容器足够高），底面半径之比为1：2，用一个管子在甲、乙两个容器的15厘米高度处连通（即管子底端离容器底15厘米）．已知只有乙容器中有水，水位高2厘米，如图所示．现同时向甲、乙两个容器注水，平均每分钟注入乙容器的水量是注入甲容器水量的k倍．开始注水1分钟，甲容器的水位上升a厘米，且比乙容器的水位低1厘米．其中a，k均为正整数，当甲、乙两个容器的水位都到达连通管子的位置时，停止注水．甲容器的水位有2次比乙容器的水位高1厘米，设注水时间为t分钟．
    （1）求k的值（用含a的代数式表示）．
    （2）当甲容器的水位第一次比乙容器的水位高1厘米时，求t的值．
    （3）当甲容器的水位第二次比乙容器的水位高1厘米时，求a，k，t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．操作探究：
    （1）现有一块等腰三角形纸板，量得周长为32cm，底比一腰多2cm．若把这个三角形纸板沿其对称轴剪开，拼成一个四边形，请画出你能拼成的各种四边形的示意图；
    （2）计算拼成的各个四边形的两条对角线长的平方和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，⊙O中，点C是优弧ACB上一点（不与A、B重合），cosC=$\frac{4}{5}$，弦AB=6，则半径r=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：${（\sqrt{3}-2）^{2015}}•{（\sqrt{3}+2）^{2016}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知
    $\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{99}$-$\frac{1}{100}$=1-$\frac{1}{100}$
    则方程$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+$\frac{x}{4×5}$+…+$\frac{x}{2015×2016}$=2015的解是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．已知$\frac{1}{p}$=$\frac{v}{m}$-2，且p≠-$\frac{1}{2}$，则m=（　　）
    A．$\frac{pv}{1+2p}$B．$\frac{pv}{1-2p}$C．$\frac{pv}{2p-1}$D．$\frac{v-2}{p}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．若（x+m）（x2-3x+n）的展开式中不含x2和x项，则m，n的值分别为（　　）
    A．m=3，n=1B．m=3，n=-9C．m=3，n=9D．m=-3，n=9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（1）分解因式：①-x3+6x2-9x；②（2a+b）2-（a+2b）2
    （2）计算：（$\frac{x+8}{{x}^{2}-4}$-$\frac{2}{x-2}$）÷$\frac{x-4}{{x}^{2}-4x+4}$
    （3）已知$\frac{x}{y}$=-2，求$\frac{x}{x-y}$-$\frac{y}{x+y}$-$\frac{{y}^{2}}{{x}^{2}-{y}^{2}}$的值．

    查看答案和解析>>

    同步练习册答案