
 如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.
如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ. 分析 注意到弦切角∠PEN=∠EQN,从而只需证明∠NEQ=∠EPN即可,而∠NEQ=∠NMP,则只需证∠NMP=∠EPN,于延长BN交PE于H,问题就转化为证明△PHN∽△MHP,即只需证PH2=HM•HN,由切割线定理可知HE2=HM•HN,从而只需证PH=HE.由CF∥BE可得$\frac{EF}{FD}=\frac{PC}{CD}$,对直线BFH截△PDE,由梅涅劳斯定理知$\frac{PH}{HE}•\frac{EF}{FD}•\frac{DB}{BP}=1$,进而有$\frac{PH}{HE}•\frac{PC}{CD}•\frac{DB}{BP}=1$,所以只需证$\frac{PC}{PB}•\frac{BD}{CD}=1$,由梅涅劳斯定理知$\frac{AS}{SC}•\frac{CP}{PB}•\frac{BT}{TA}=1$,结合切线长定理易知$\frac{PC}{PB}•\frac{BD}{CD}=1$成立,故原命题成立.
解答 证明:如图,设⊙I与AC、AB分别切于点S、T,连接ST、AI、IT,设ST与AI交于点G.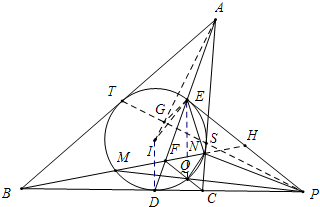
则IE⊥PE,ID⊥PD,故I、E、P、D四点共圆,
∴I、G、E、P、D五点共圆,
∴∠IGP=∠IEP=90°,即IG⊥PG,
∴P、S、T三点共线,
对直线PST截△ABC,由梅涅劳斯定理知$\frac{AS}{SC}•\frac{CP}{PB}•\frac{BT}{TA}=1$,
∵AS=AT,CS=CD,BT=BD,
∴$\frac{PC}{PB}•\frac{BD}{CD}=1$,
设BN的延长线与PE交于点H,对直线BFH截△PDE,由梅涅劳斯定理知$\frac{PH}{HE}•\frac{EF}{FD}•\frac{DB}{BP}=1$,
∵CF∥BE,
∴$\frac{EF}{FD}=\frac{PC}{CD}$,
∴$\frac{PH}{HE}•\frac{PC}{CD}•\frac{DB}{BP}=1$,
∴PH=HE,
∴PH2=HE2=HM•HN,
∴$\frac{PH}{HM}=\frac{HN}{PH}$,
∴△PHN∽△MHP,
∴∠HPN=∠HMP=∠NEQ,
∵∠PEN=∠EQN,
∴∠ENP=∠ENQ.
点评 本题主要考查了四点共圆的判定与性质、圆的切线性质、相似三角形的判定与性质、梅涅劳斯定理的应用,难度很大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,CD⊥AB.垂足为D,E是AC的中点,ED、CB的延长线于点F.
如图,在△ABC中,∠ACB=90°,CD⊥AB.垂足为D,E是AC的中点,ED、CB的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
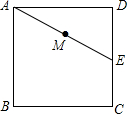 如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.
如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.
如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com