
����Ŀ��ij����������һ����ɫ��Ʒ�������飬��16000Ԫ�ɹ�A����Ʒ�ļ�������7500Ԫ�ɹ�B����Ʒ�ļ�����2����һ��A����Ʒ�Ľ��۱�һ��B����Ʒ�Ľ��۶�10Ԫ��
��1����һ��A��B����Ʒ�Ľ��۷ֱ��Ƕ��٣�
��2���������̹���A��B����Ʒ��250��������A����Ʒ�ۼ�Ϊ240Ԫ/����B����Ʒ�ۼ�Ϊ220Ԫ/������ȫ���۳�����֪����B����Ʒm����A����Ʒ�ļ�����С��B����Ʒ�ļ�������B����Ʒ��������С��80��������������������Ʒ���������
���𰸡���1��һ��A��B����Ʒ�Ľ��۷ֱ���160Ԫ��150Ԫ����2��������������Ʒ�����������19200Ԫ
��������
��1��������������г���Ӧ�ķ�ʽ���̣��Ӷ��������һ��A��B����Ʒ�Ľ��۷ֱ��Ƕ���Ԫ��ע���ʽ����Ҫ���飻
��2������������Եõ�������m�ĺ�����ϵ���ٸ���A����Ʒ�ļ�����С��B����Ʒ�ļ�������B����Ʒ��������С��80�������Եõ�����m�IJ���ʽ�飬�Ӷ��������m��ȡֵ��Χ���Ӷ����������������ֵ��
��1����һ��B����Ʒ�Ľ���ΪxԪ����һ��A����Ʒ�Ľ���Ϊ��x+10��Ԫ��
![]()
��ã�x=150��
�����飬x=150��ԭ��ʽ���̵Ľ⣬
��x+10=160��
��һ��A��B����Ʒ�Ľ��۷ֱ���160Ԫ��150Ԫ��
��2����������������Ʒ������ΪwԪ��
w=��240��160����250��m��+��220��150��m=��10m+20000��
��A����Ʒ�ļ�����С��B����Ʒ�ļ�������B����Ʒ��������С��80����
��![]() ����80��m��125��
����80��m��125��
�൱m=80ʱ��wȡ�����ֵ����ʱw=��10��80+20000=19200��
��������������Ʒ�����������19200Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����֪������
����֪������![]() ��
��![]() ��������ҽ���
��������ҽ���![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
![]() �������߹���
�������߹���![]() ���������ߵĽ���ʽ��
���������ߵĽ���ʽ��
![]() �ڵڶ������ڵ����������Ƿ���ڵ�
�ڵڶ������ڵ����������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() �����������������
����Ϊ�������������![]() ���ƣ������ڣ���
���ƣ������ڣ���![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
![]() ��ͼ
��ͼ![]() ����
����![]() �������£���
�������£���![]() ������Ϊ
������Ϊ![]() ����
����![]() ���������ϵĵ㣬��
���������ϵĵ㣬��![]() ���ϣ�����������
���ϣ�����������![]() ��
��![]() ���㣬��
���㣬��![]() ����
����![]() ��
��![]() �����ƶ����δ�ʱ���ı���
�����ƶ����δ�ʱ���ı���![]() ���ܳ���С����ֱ��д�����������ĵ�
���ܳ���С����ֱ��д�����������ĵ�![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�й�������![]() �ġ�
�ġ�![]() �͡�
�͡�![]() ���ǵȱ������Σ���
���ǵȱ������Σ���![]() ��
��![]() .
.

(1)��ͼ1������![]() ǡ����
ǡ����![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
����֤��![]() ��
��
������![]() ����֤��
����֤��![]() ��
��![]() ��
��
(2)ͼ2����ͼ1�еġ�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת��
˳ʱ����ת��![]() (
(![]() ��
��![]() ��
��![]() )�õ���ʹ��
)�õ���ʹ��![]() ǡ�þ���
ǡ�þ���![]() ���е�
���е�![]() ���Բ����߶�
���Բ����߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
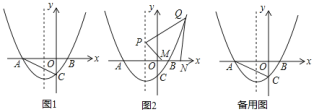
����Ŀ����ͼ��������y=ax2+bx+c����A����5��0����B��1��0����C��0��![]() ������
������
��1����գ������ߵĽ���ʽ��������
��2�����������ߵĶԳ�������һ��P��ʹPB+PC��ֵ��С�����P�����ꣻ
�ڵ�MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��B��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С��һ�ҳ�������ǰ��ij�����Σ��ƻ��ڶ�����������Դ�����Լݳ��Ρ�
 [��
[��
����������Ϣ������������⣺
��1�����ʱ��Ϊ![]() Сʱ�����ü�˾�ij��������Ϊ
Сʱ�����ü�˾�ij��������Ϊ![]() Ԫ�������ҹ�˾�ij��������Ϊ
Ԫ�������ҹ�˾�ij��������Ϊ![]() Ԫ���ֱ����
Ԫ���ֱ����![]() ��
��![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������С�����㲢ѡ���ĸ����η������㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC�У���D�ڱ�AC�ϣ����������У����жϡ�BDC���ABC���Ƶ��� ( )

A. AB��CB=CA��CD B. AB��CD=BD��BC C. BC2=AC��DC D. BD2=CD��DA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������١�A=45�㣬AB=12��AC=15����A��=45�㣬A��B��=16��A��C��=20���ڡ�A=47�㣬AB=1.5��AC=2����B��=47�㣬A��B��=2.8��B��C��=2.1���ۡ�A=47�㣬AB=2��AC=3����B��=47�㣬A��B��=4��B��C��=6���������ж���ABC����A��B��C�����Ƶ��� ( )
A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ںڰ���д�²����� ![]() ����������ÿ��ֻ��дһ���������涨��ֹ�ںڰ���д�Ѿ�д��������Լ���������д��Ϊʧ���ߣ������д��һ������ô����д������ ��ʱ�б�ʤ�IJ��ԣ�
����������ÿ��ֻ��дһ���������涨��ֹ�ںڰ���д�Ѿ�д��������Լ���������д��Ϊʧ���ߣ������д��һ������ô����д������ ��ʱ�б�ʤ�IJ��ԣ�
A. 10 B. 9 C. 8D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ�������µ����⣺
��1����������ABC��![]() ����
����![]() �Ķ��������𰸣�35����
�Ķ��������𰸣�35����
��2����������ABC��![]() ����
����![]() �Ķ��������𰸣�40����70����100����
�Ķ��������𰸣�40����70����100����
����ʦ����ͬѧ�DZ��⣬С�ձ�������һ�⣺
��1������������ABC��![]() ����
����![]() �Ķ���Ϊ______����2��С�շ��֣�
�Ķ���Ϊ______����2��С�շ��֣�![]() �Ķ�����ͬ���õ�
�Ķ�����ͬ���õ�![]() �Ķ����ĸ���Ҳ���ܲ�ͬ������ڵ���������ABC�У���
�Ķ����ĸ���Ҳ���ܲ�ͬ������ڵ���������ABC�У���![]() ����
����![]() ��������ͬ�Ķ���ʱ��x��ȡֵ��Χ��______��
��������ͬ�Ķ���ʱ��x��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com