
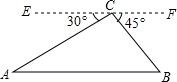
 如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. 分析 如图,过点C作CD⊥AB于点D,构建直角△ACD和直角△BCD,通过解这两个直角三角形求AD、BD的长度,则易求AB=AD+BD.
解答 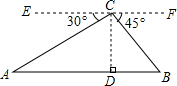 解:如图,过点C作CD⊥AB于点D,
解:如图,过点C作CD⊥AB于点D,
在直角△ACD中,∠A=30°,AC=400米,则AD=AC•cos30°=400×$\frac{\sqrt{3}}{2}$=200$\sqrt{3}$(米),CD=$\frac{1}{2}$AC=200米.
在直角△BCD中,∠B=45°,∠CDB=90°,则∠BCD=∠B=45°,
所以BD=CD=200米,
所以AB=AD+BD=200$\sqrt{3}$+200(米).
点评 此题考查了解直角三角形的应用-仰角俯角问题,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3m2n2与-m2n3 | B. | $\frac{1}{2}$xy与2yx | C. | 53与a3 | D. | 3x2y2与4x2z2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 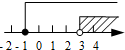 | C. | 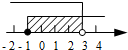 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
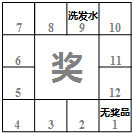 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | x<$\frac{1}{4}$ | C. | $\frac{1}{4}$<x<1 | D. | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com