
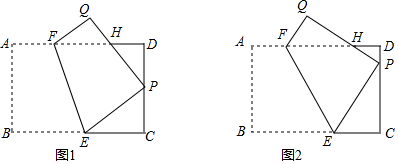
分析 (1)由题意可知PC=3,由翻折的性质可知BE=PE,设EC=x,则PE=9-x,在Rt△PEC中,依据勾股定理列方程求解即可;
(2)依据含30°直角三角形的性质可知:EC=$\frac{1}{2}$PE,设EC=x,则EB=9-x,由翻折的性质可知EP=BE=9-x,列出关于x的方程可求得EC的长,然后利用特殊锐角三角函数值,可求得PC、PD、DH的长,然后设AF=y,由翻折的性质可知AF=QF=y,最后依据FQ=$\frac{1}{2}$FH列方程求解即可;
(3)连结EH,先求得FH和PH、PE的长,最后依据四边形FEPH的面积=△FHE的面积+△HPE的面积求解即可.
解答 解:(1)∵ABCD为矩形,
∴CD=AB=6.
∵P是DC的中点,
∴PC=3.
由翻折的性质可知BE=PE.
设EC=x,则PE=9-x.
在Rt△PEC中,依据勾股定理可知:PE2=EC2+PC2,即(9-x)2=x2+32,解得:x=4,
∴EC=4.
(2)∵∠CPE=30°,∠C=90°,
∴EC=$\frac{1}{2}$PE.
设EC=x,则EB=9-x,由翻折的性质可知EP=BE=9-x.
∵EC=$\frac{1}{2}$PE,
∴x=$\frac{1}{2}$×(9-x).
解得:x=3.
∴EC=3.
∴$\frac{EC}{PC}$=tan60°=$\frac{\sqrt{3}}{3}$,则CP=3$\sqrt{3}$.
∴DP=6-3$\sqrt{3}$.
∵∠EPH=90°,∠CPE=30°,
∴∠DPH=60°.
∴DH=$\sqrt{3}$DP=6$\sqrt{3}$-9.
∴AH=18-6$\sqrt{3}$.
设AF=y,由翻折的性质可知AF=QF=y,则FH=18-6$\sqrt{3}$-y.
∵∠QHF=30°,∠Q=90°,
∴QF=$\frac{1}{2}$FH.
∴y=$\frac{1}{2}$×(18-6$\sqrt{3}$-y),解得:y=6-2$\sqrt{3}$.
∴AF=6-2$\sqrt{3}$.
(3)如图所示:连结EH.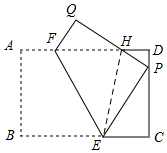
由(2)可知AF=6-2$\sqrt{3}$,
∴FH=18-6$\sqrt{3}$-(6-2$\sqrt{3}$)=12-4$\sqrt{3}$.
∵PH=2DP,EP=2EC,
∴PH=12-6$\sqrt{3}$,PE=6.
∴四边形FEPH的面积=△FHE的面积+△HPE的面积=$\frac{1}{2}$FH•AB+$\frac{1}{2}$HP•EP
=$\frac{1}{2}×$(12-4$\sqrt{3}$)×6+$\frac{1}{2}$×(12-6$\sqrt{3}$)×6=72-30$\sqrt{3}$.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了矩形的性质、特殊锐角三角函数值、翻折的性质,解答本题的关键是利用特殊锐角三角函数值求得相关线段的长,同时连结HE将四边形的面积转为两个三角形的面积之和求解是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
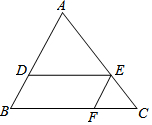 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则$\frac{{S}_{△EFC}}{{S}_{?BFED}}$的值为( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则$\frac{{S}_{△EFC}}{{S}_{?BFED}}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
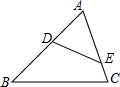 在△ABC与△AED中,$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则S△ADE:S△ABC的值为( )
在△ABC与△AED中,$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则S△ADE:S△ABC的值为( )| A. | $1:\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D、E分别在边AB、BC边上,且BD=6cm,BA=9cm,BE=4cm,若DE平行于AC,则EC=( )
如图,在△ABC中,点D、E分别在边AB、BC边上,且BD=6cm,BA=9cm,BE=4cm,若DE平行于AC,则EC=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购进甲种服装的数量/件 | 10 | 20 | x |
| 购进甲种服装所用费用/元 | 800 | 1600 | 80x |
| 购进乙种服装所用费用/元 | 5400 | 4800 | 6000-60x |
| 购进甲种服装的数量/件 | 10 | 20 | x |
| 甲种服装获得的利润/元 | 400 | 800 | 40x |
| 乙种服装获得的利润/元 | 2700 | 2400 | 3000-30x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com