
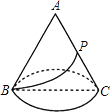
【题目】如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速行动,速度为
方向匀速行动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停让运动.连接
;当一个点停止运动,另一个点也停让运动.连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,解答下列问题:
,解答下列问题:
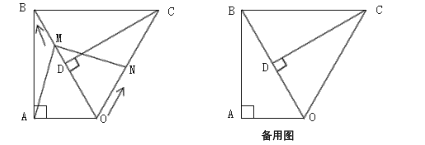
(1)当![]() 为何值时,
为何值时,![]() 平分
平分![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函教关系式;
的函教关系式;
(3)在运动过程中,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 为线段
为线段![]() 的中点?若存在,求出
的中点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
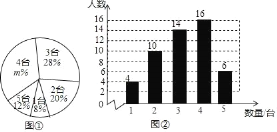
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系内,A,B为x轴上两点,以AB为直径的⊙M交y轴于C,D两点,C为![]() 的中点,弦AE交y轴于点F,且点A的坐标为(2,0),CD=8
的中点,弦AE交y轴于点F,且点A的坐标为(2,0),CD=8
(1)求⊙M的半径;
(2)动点P在⊙M的圆周上运动.
①如图1,当FP的长度最大时,点P记为P,在图1中画出点P0,并求出点P0横坐标a的值;
②如图1,当EP平分∠AEB时,求EP的长度;
③如图2,过点D作⊙M的切线交x轴于点Q,当点P与点A,B不重合时,请证明![]() 为定值.
为定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
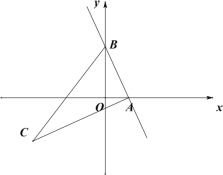
【题目】如图所示,已知直线![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 与点
与点![]() ,点
,点![]() 在第三象限内,且
在第三象限内,且![]() ,
,![]() .
.
(1)当![]() 时,求抛物线的表达式;
时,求抛物线的表达式;
(2)设点![]() 坐标为
坐标为![]() ,试用
,试用![]() 分别表示
分别表示![]() ;
;
(3)记![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为____________.
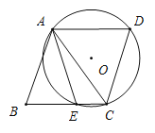
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情过后,为了促进消费,某商场设计了一种促销活动:在一个不透明的箱子里放有四个相同的小球,球上分别标有“10元”、“20元”、“30元”和“40元”的字样,规定:在本商场同一日内,顾客每消费满500元,就可以在箱子里先后摸出两个球(第一次摸出后不放回)。商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费500元.
(1)该顺客最多可得到______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于60元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com