
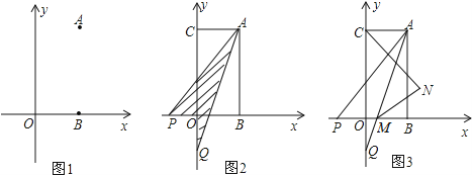
【题目】如图:已知在平面直角坐标系中点A(a,b)点B(a,0),且满足|2a-b|+(b-4)2=0.
(1)求点A、点B的坐标;
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动.同时点Q从C点出发,沿y轴负方向以2个单位每秒的速度移动,某一时刻,如图所示且S阴=![]() S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;
(3)在(2)的条件下,AQ交x轴于M,作∠ACO,∠AMB的角平分线交于点N,判断![]() 是否
是否![]() 为定值,若是定值求其值;若不是定值,说明理由.
为定值,若是定值求其值;若不是定值,说明理由.
【答案】(1)点A(2,4)、点B(2,0);(2)3s;(3)是定值,![]()
【解析】
(1)根据非负数的性质易得a=2,b=4,则点A的坐标为(2,4)、点B的坐标(2,0);
(2)设P点运动时间为t,则t>2,则P点坐标可表示为(2-t,0),Q点坐标表示为(0,4-2t),用待定系数法确定直线AQ的解析式为y=tx+4-2t,则可确定直线AQ与x轴交点坐标为(![]() ,0),根据题意得
,0),根据题意得![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4)=
×(2t-4)=![]() ×2×4,然后解方程求出t的值;
×2×4,然后解方程求出t的值;
(3)先根据角平分线定义得∠ACN=45°,∠1=∠2,再由AC∥BP得∠CAM=∠AMB=2∠1,然后根据三角形内角和定理得∠ACN+∠CAM=∠N+∠1,所以∠N=45°+∠1,再根据三角形外角性质得∠AMB=∠APB+∠PAQ,即∠APB+∠PAQ=2∠1,接着根据三角形内角和定理得∠AQC+∠OMQ=90°,利用∠OMQ=2∠1可得∠AQC=90°-2∠1,最后用∠1表示式子![]() 中的角,约分即可得到
中的角,约分即可得到![]() =
=![]() .
.
解:(1)∵|2a-b|+(b-4)2=0.
∴2a-b=0,b-4=0,
∴a=2,b=4,
∴点A的坐标为(2,4)、点B的坐标(2,0);
(2)如图2,设P点运动时间为t,则t>2,所以P点坐标为(2-t,0),Q点坐标为(0,4-2t),
设直线AQ的解析式为y=kx+4-2t,
把A(2,4)代入得2k+4-2t=4,解得k=t,
∴直线AQ的解析式为y=tx+4-2t,
直线AQ与x轴交点坐标为(![]() ,0),
,0),
∴S阴影=![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4),
×(2t-4),
而S阴=![]() S四边形OCAB,
S四边形OCAB,
∴![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4)=
×(2t-4)=![]() ×2×4,
×2×4,
整理得t2-3t=0,
解得t1=0(舍去),t2=3,
∴点P移动的时间为3s;
(3)![]() 为定值.理由如下:
为定值.理由如下:
如图3,∵∠ACO,∠AMB的角平分线交于点N,
∴∠ACN=45°,∠1=∠2,
∵AC∥BP,
∴∠CAM=∠AMB=2∠1,
∵∠ACN+∠CAM=∠N+∠1,
∴45°+2∠1=∠N+∠1,
∴∠N=45°+∠1,
∵∠AMB=∠APB+∠PAQ,
∴∠APB+∠PAQ=2∠1,
∵∠AQC+∠OMQ=90°,
而∠OMQ=2∠1,
∴∠AQC=90°-2∠1,
∴![]() =
=![]() =
=![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
![]() 将图1中的三角板绕点O以每秒
将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周
的速度沿逆时针方向旋转一周![]() 如图2,经过t秒后,ON落在OC边上,则
如图2,经过t秒后,ON落在OC边上,则![]() ______秒
______秒![]() 直接写结果
直接写结果![]() .
.
![]() 如图2,三角板继续绕点O以每秒
如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上
的速度沿逆时针方向旋转到起点OA上![]() 同时射线OC也绕O点以每秒
同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
![]() 当OC转动9秒时,求
当OC转动9秒时,求![]() 的度数.
的度数.
![]() 运动多少秒时,
运动多少秒时,![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC的平分线与BC的垂直平分线PQ相交于点P,PM⊥AC,PN⊥AB,垂足分别为M、N,AB=5,AC=11,则CM的长度为( )
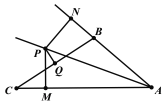
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
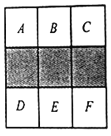
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现将方格内空白的小正方形(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
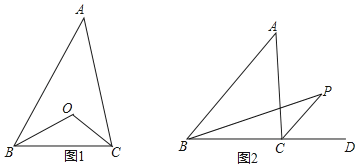
【题目】(1)如图1,△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=56°,求∠BOC的度数;
(2)如图2,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,先写出∠A和∠P的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道![]() 有以下两个方案:
有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最![]() 短在途中标出M、N的位置,保留画图痕迹;
短在途中标出M、N的位置,保留画图痕迹;

设方案一中铺设的支管道总长度为L1![]() ,方案二中铺设的支管道总长度为
,方案二中铺设的支管道总长度为![]() ,则L1与L2的大小关系为: L1_____ L2(填
,则L1与L2的大小关系为: L1_____ L2(填![]() ”、
”、![]() ”或)理由是______.
”或)理由是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深入践行素质教育,落实学生的核心素养,培养全面发展的人,育红中学积极开展校本课程建设,促进学生的个性发展,计划成立“![]() .陶艺社团、
.陶艺社团、![]() .航模社团、
.航模社团、![]() .足球社团、
.足球社团、![]() .
.![]() 科技社团、
科技社团、![]() .其他”,规定每位学生选报一个.为了了解报名情况,随机抽取了部分学生进行调查,将所有调查结果整理后绘制成不完整的条形统计图(如图1)和扇形统计图(如图2),请结合统计图回答下列问题:
.其他”,规定每位学生选报一个.为了了解报名情况,随机抽取了部分学生进行调查,将所有调查结果整理后绘制成不完整的条形统计图(如图1)和扇形统计图(如图2),请结合统计图回答下列问题:
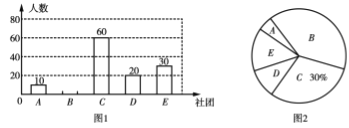
(1)在这次调查中,一共调查了_______名学生;
(2)扇形统计图中,扇形![]() 的圆心角度数是_______;
的圆心角度数是_______;
(3)请补全条形统计图;
(4)若该校共有6800名学生,请估计全校选择“![]() 科技社团”的学生人数.
科技社团”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y(m)与时间t(s)的函数图象是( )
A. 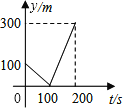 B.
B. 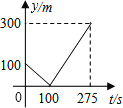
C. 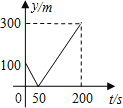 D.
D. 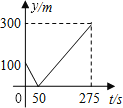
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com