
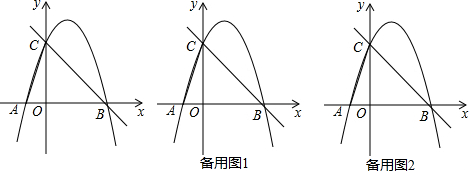
分析 (1)利用直线BC的解析式求出点B、C的坐标,然后代入y=-x2+bx+c即可求出b和C的值;
(2)由于点E的不确定性,所以点E的位置由两种情况,一种是点E在直线BC上方,另一种是点E在直线BC的下方,利用三角形面积公式即可答案;
(3)由(2)可知点E的情况有两种,当点E在直线BC上方时,由于点Q关于x轴的对称点在抛物线,所以点p只能在B的左侧;当点E在直线BC下方时,有三种情况,其中点E在第二、三象限时不满足题意,所以点E只能在第四象限.
解答 解:(1)令x=0代入y=-x+3,
∴y=3,
∴点C的坐标为(0,3),
令y=0,代入y=-x+3,
∴x=3,
∴点B的坐标为(3,0),
把B(3,0)和C(0,3)代入y=-x2+bx+c,
∴$\left\{\begin{array}{l}{c=3}\\{0=-9+3b+c}\end{array}\right.$
∴解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3,
(2) 当点E在直线BC上方时,
当点E在直线BC上方时,
过点E作EF⊥x轴于点F,交BC于点G,
∵E的横坐标为m,
∴令x=m代入y=-x+3,
∴y=3-m,
∴点G的坐标为(m,3-m),
令x=m代入y=-x2+2x+3,
∴y=-m2+2m+3,
∴点E的坐标为(m,-m2+2m+3)
∴GE=-m2+3m,
∴S=$\frac{1}{2}$GE•OF+$\frac{1}{2}$GE•BF=$\frac{1}{2}$GE•OB=$\frac{1}{2}$×3(-m2+3m)=-$\frac{3}{2}$m2+$\frac{9}{2}$m,
当点E在直线BC下方时,如图2,
过点E作EF⊥y轴于点G,交BC于点F,
∵点E的坐标为(m,-m2+2m+3)
∴点F的纵坐标为-m2+2m+3,
令y=-m2+2m+3代入y=-x+3,
∴x=m2-2m,
∴F的坐标为(m2-2m,-m2+2m+3),
∴EF=m2-2m-m=m2-3m,
∴S=$\frac{1}{2}$EF•CG=$\frac{1}{2}$EF•OG=$\frac{1}{2}$EF•OC=$\frac{3}{2}$(m2-3m)=$\frac{3}{2}$m2-$\frac{9}{2}$m,
综上所述,S与m的函数关系式为S=-$\frac{3}{2}$m2+$\frac{9}{2}$m或S=$\frac{3}{2}$m2-$\frac{9}{2}$m;
(3)当点E在直线BC的上方时,如图3,
若点P在B的左侧时,此时点Q关于x轴的对称点不在抛物线上,
∴点P只能在点B右侧,
设抛物线的对称轴与x轴交于点H,BP的垂直平分线交x轴于点M,
∵$\frac{LQ}{AP}=\frac{5}{8}$,
∴设LQ=5t,AP=8t,
令y=0代入y=-x2+2x+3,
解得:x=-1或x=3,
∴A(-1,0)
∴AB=4,
∴BP=AP-AB=8t-4,
∴BM=$\frac{1}{2}$BP=4t-2,
∵HB=2,
∴HM=LK=HB+BM=4t,
∴cos∠QAM=cos∠QLK=$\frac{LK}{LQ}$=$\frac{4}{5}$,
∴$\frac{3}{4}$AM=QM,
设Q的横坐标为q,
∴AM=q+1,
∵点Q关于x轴的对称点在抛物线上,
∴QM=-(-q2+2q+3),
∴$\frac{3}{4}$(q+1)=-(-q2+2q+3),
解得:q=-1或q=$\frac{15}{4}$,
当q=-1时,
M与Q重合,舍去,
当q=$\frac{15}{4}$时,
∴OP=OB+BP=2q-3=$\frac{9}{2}$,
∴点P坐标为($\frac{9}{2}$,0)
当点E在直线BC的下方时,如图4
若点E在第二象限时,则此时点Q的对称点不在抛物线上,
若点E在第三象限时,则此时射线AE与抛物线的对称轴无交点,
所以点E只能在第四象限,
由于点Q关于x轴的对称点在抛物线上,
∴点P在B的左侧,
设抛物线的对称轴与x轴交于点H,BP的垂直平分线与x轴交于点M,
过点L作LK∥x轴,交MQ于点K,
∴易求得:KL=HM=4t,
∴cos∠QAM=∠QLK=$\frac{4}{5}$,
∴$\frac{3}{4}$AM=QM,
设Q的横坐标为q,
∴AM=q+1,
∵点Q关于x轴的对称点在抛物线上
∴QM=-q2+2q+3,
∴$\frac{3}{4}$(q+1)=-q2+2q+3,
解得:q=-1或q=$\frac{9}{4}$,
∴q=-1时,
此时M与Q重合,舍去,
当q=$\frac{9}{4}$时,
∴OP=q-(3-q)=$\frac{3}{2}$,
∴点P的坐标为($\frac{3}{2}$,0)
综上所述,点P的坐标为($\frac{9}{2}$,0)或($\frac{3}{2}$,0).
点评 本题考查二次函数的综合问题,涉及待定系数法求解析式,轴对称的性质,解方程等知识,考查知识综合程度高,需要学生灵活运用所学知识进行解答,


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
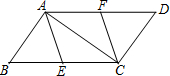 如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,
如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
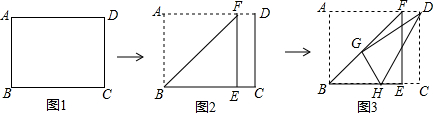
 如图,△ABC的中位线DE=10cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是16cm,则△ABC的面积为160cm2.
如图,△ABC的中位线DE=10cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是16cm,则△ABC的面积为160cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
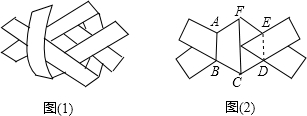 用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm.
用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com