
”¾ĢāÄæ”æČēĶ¼£¬µćBŌŚĻ߶ĪACÉĻ£¬µćD”¢EŌŚACĶ¬²ą£¬”ĻA=”ĻC=90”ć£¬BD”ĶBE£¬AD=BC£® 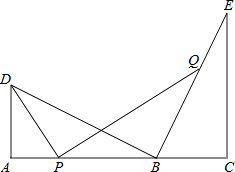
£Ø1£©ĒóÖ¤£ŗAC=AD+CE£»
£Ø2£©ČōAD=3£¬CE=5£¬µćPĪŖĻ߶ĪABÉĻµÄ¶Æµć£¬Į¬½ÓDP£¬×÷PQ”ĶDP£¬½»Ö±ĻßBEÓŚµćQ£» £Øi£©µ±µćPÓėA”¢BĮ½µć²»ÖŲŗĻŹ±£¬Ēó ![]() µÄÖµ£»
掙术
£Øii£©µ±µćP“ÓAµćŌĖ¶Æµ½ACµÄÖŠµćŹ±£¬ĒóĻ߶ĪDQµÄÖŠµćĖł¾¹żµÄĀ·¾¶£ØĻ߶Ī£©³¤£®£ØÖ±½ÓŠ“³ö½į¹ū£¬²»±ŲŠ“³ö½ā“š¹ż³Ģ£©
”¾“š°ø”æ
£Ø1£©Ö¤Ć÷£ŗ”ßBD”ĶBE£¬
”ą”Ļ1+”Ļ2=180”ć©90”ć=90”ć£¬
”ß”ĻC=90”ć£¬
”ą”Ļ2+”ĻE=180”ć©90”ć=90”ć£¬
”ą”Ļ1=”ĻE£¬
”ßŌŚ”÷ABDŗĶ”÷CEBÖŠ£¬
 £¬
£¬
”ą”÷ABD”Õ”÷CEB£ØAAS£©£¬
”ąAB=CE£¬
”ąAC=AB+BC=AD+CE
£Ø2£©£Øi£©ČēĶ¼£¬¹żµćQ×÷QF”ĶBCÓŚF£¬
Ōņ”÷BFQ”×”÷BCE£¬
”ą ![]() £¬
£¬
¼“ ![]() £¬
£¬
”ąQF= ![]() BF£¬
BF£¬
”ßDP”ĶPQ£¬
”ą”ĻAPD+”ĻFPQ=180”ć©90”ć=90”ć£¬
”ß”ĻAPD+”ĻADP=180”ć©90”ć=90”ć£¬
”ą”ĻADP=”ĻFPQ£¬
Ó֔ߔĻA=”ĻPFQ=90”ć£¬
”ą”÷ADP”×”÷FPQ£¬
”ą ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ą5AP©AP2+APBF=3 ![]() BF£¬
BF£¬
ÕūĄķµĆ£¬£ØAP©BF£©£ØAP©5£©=0£¬
”ßµćPÓėA£¬BĮ½µć²»ÖŲŗĻ£¬
”ąAP”Ł5£¬
”ąAP=BF£¬
ÓÉ”÷ADP”×”÷FPQµĆ£¬ ![]() =
= ![]() £¬
£¬
”ą ![]() =
= ![]() £»
£»
£Øii£©Ļ߶ĪDQµÄÖŠµćĖł¾¹żµÄĀ·¾¶£ØĻ߶Ī£©¾ĶŹĒ”÷BDQµÄÖŠĪ»ĻßMN£®
ÓÉ£Ø2£©£Øi£©æÉÖŖ£¬QF= ![]() AP£®
AP£®
µ±µćPŌĖ¶ÆÖĮACÖŠµćŹ±£¬AP=4£¬”ąQF= ![]() £®
£®
”ąBF=QF”Į ![]() =4£®
=4£®
ŌŚRt”÷BFQÖŠ£¬øł¾Ż¹“¹É¶ØĄķµĆ£ŗBQ= ![]() =
= ![]() =
= ![]() £®
£®
”ąMN= ![]() BQ=
BQ= ![]() £®
£®
”ąĻ߶ĪDQµÄÖŠµćĖł¾¹żµÄĀ·¾¶£ØĻ߶Ī£©³¤ĪŖ ![]() £®
£®


”¾½āĪö”æ£Ø1£©øł¾ŻĶ¬½ĒµÄÓą½ĒĻąµČĒó³ö”Ļ1=”ĻE£¬ŌŁĄūÓĆ”°½Ē½Ē±ß”±Ö¤Ć÷”÷ABDŗĶ”÷CBČ«µČ£¬øł¾ŻČ«µČČż½ĒŠĪ¶ŌÓ¦±ßĻąµČæɵĆAB=CE£¬Č»ŗóøł¾ŻAC=AB+BCÕūĄķ¼“æɵĆÖ¤£»£Ø2£©£Øi£©¹żµćQ×÷QF”ĶBCÓŚF£¬øł¾Ż”÷BFQŗĶ”÷BCEĻąĖĘæÉµĆ ![]() £¬Č»ŗóĒó³öQF=
£¬Č»ŗóĒó³öQF= ![]() BF£¬ŌŁøł¾Ż”÷ADPŗĶ”÷FPQĻąĖĘæɵĆ
BF£¬ŌŁøł¾Ż”÷ADPŗĶ”÷FPQĻąĖĘæÉµĆ ![]() =
= ![]() £¬Č»ŗóÕūĄķµĆµ½£ØAP©BF£©£Ø5©AP£©=0£¬“Ó¶ųĒó³öAP=BF£¬×īŗóĄūÓĆĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżæɵĆ
£¬Č»ŗóÕūĄķµĆµ½£ØAP©BF£©£Ø5©AP£©=0£¬“Ó¶ųĒó³öAP=BF£¬×īŗóĄūÓĆĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżæÉµĆ ![]() =
= ![]() £¬“Ó¶ųµĆ½ā£»£Øii£©ÅŠ¶Ļ³öDQµÄÖŠµćµÄĀ·¾¶ĪŖ”÷BDQµÄÖŠĪ»ĻßMN£®Ēó³öQF”¢BFµÄ³¤¶Č£¬ĄūÓĆ¹“¹É¶ØĄķĒó³öBQµÄ³¤¶Č£¬ŌŁøł¾ŻÖŠĪ»ĻߊŌÖŹĒó³öMNµÄ³¤¶Č£¬¼“ĖłĒóÖ®Ā·¾¶³¤£®
£¬“Ó¶ųµĆ½ā£»£Øii£©ÅŠ¶Ļ³öDQµÄÖŠµćµÄĀ·¾¶ĪŖ”÷BDQµÄÖŠĪ»ĻßMN£®Ēó³öQF”¢BFµÄ³¤¶Č£¬ĄūÓĆ¹“¹É¶ØĄķĒó³öBQµÄ³¤¶Č£¬ŌŁøł¾ŻÖŠĪ»ĻߊŌÖŹĒó³öMNµÄ³¤¶Č£¬¼“ĖłĒóÖ®Ā·¾¶³¤£®
”¾æ¼µć¾«Īö”æĶعżĮé»īŌĖÓĆĻąĖĘČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬ÕĘĪÕĻąĖĘČż½ĒŠĪµÄŅ»ĒŠ¶ŌÓ¦Ļ߶Ī(¶ŌÓ¦øß”¢¶ŌÓ¦ÖŠĻß”¢¶ŌÓ¦½ĒĘ½·ÖĻß”¢Ķā½ÓŌ²°ė¾¶”¢ÄŚĒŠŌ²°ė¾¶µČ£©µÄ±ČµČÓŚĻąĖĘ±Č£»ĻąĖĘČż½ĒŠĪÖܳ¤µÄ±ČµČÓŚĻąĖĘ±Č£»ĻąĖĘČż½ĒŠĪĆ껿µÄ±ČµČÓŚĻąĖʱȵÄĘ½·½¼“æÉŅŌ½ā“š“ĖĢā£®


 ¼ĘĖćøߏÖĻµĮŠ“š°ø
¼ĘĖćøߏÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ·½±ćŹŠĆń³öŠŠ£¬¼õĒį³ĒŹŠÖŠŠÄ½»ĶØŃ¹Į¦£¬Ä³ŹŠÕżŌŚŠŽ½Ø¹į“©Č«³ĒÄĻ±±”¢¶«Ī÷µÄµŲĢś1£¬2ŗÅĻߣ®ŅŃÖŖŠŽ½ØµŲĢś1ŗÅĻß24Ē§Ć×ŗĶ2ŗÅĻß22Ē§Ć×¹²ŠčĶ¶×Ź265ŅŚŌŖ£¬ĒŅ1ŗÅĻßĆæĒ§Ć×µÄĘ½¾łŌģ¼Ū±Č2ŗÅĻßĆæĒ§Ć×µÄĘ½¾łŌģ¼Ū¶ą0.5ŅŚŌŖ£®
(1)Ēó1ŗÅĻß”¢2ŗÅĻßĆæĒ§Ć×µÄĘ½¾łŌģ¼Ū·Ö±šŹĒ¶ąÉŁŅŚŌŖ£»
(2)³ż1£¬2ŗÅĻßĶā£¬øĆŹŠ¹ę»®µ½2019Äź»¹ŅŖŌŁ½Ø91.8Ē§Ć׵ĵŲĢśĻßĶų£®¾ŻŌ¤Ėć£¬Õā91.8Ē§Ć×µŲĢśĻßĶųĆæĒ§Ć×µÄĘ½¾łŌģ¼ŪŹĒ1ŗÅĻßĆæĒ§Ć×µÄĘ½¾łŌģ¼ŪµÄ1.2±¶£¬Ōņ»¹ŠčĶ¶×Ź¶ąÉŁŅŚŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¾ŲŠĪOABCÖŠ£¬OA=2£¬AB=4£¬Ė«ĒśĻß ![]() £Øk£¾0£©Óė¾ŲŠĪĮ½±ßAB”¢BC·Ö±š½»ÓŚE”¢F£®
£Øk£¾0£©Óė¾ŲŠĪĮ½±ßAB”¢BC·Ö±š½»ÓŚE”¢F£®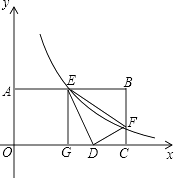
£Ø1£©ČōEŹĒABµÄÖŠµć£¬ĒóFµćµÄ×ų±ź£»
£Ø2£©Čō½«”÷BEFŃŲÖ±ĻßEF¶ŌÕŪ£¬BµćĀäŌŚxÖįÉĻµÄDµć£¬×÷EG”ĶOC£¬“¹×ćĪŖG£¬Ö¤Ć÷”÷EGD”×”÷DCF£¬²¢ĒókµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßy=kx£ØkĪŖ³£Źż£©ÓėÅ×ĪļĻßy= ![]() x2©2½»ÓŚA£¬BĮ½µć£¬ĒŅAµćŌŚyÖį×ó²ą£¬PµćµÄ×ų±źĪŖ£Ø0£¬©4£©£¬Į¬½ÓPA£¬PB£®ÓŠŅŌĻĀĖµ·Ø£ŗ
x2©2½»ÓŚA£¬BĮ½µć£¬ĒŅAµćŌŚyÖį×ó²ą£¬PµćµÄ×ų±źĪŖ£Ø0£¬©4£©£¬Į¬½ÓPA£¬PB£®ÓŠŅŌĻĀĖµ·Ø£ŗ
¢ŁPO2=PAPB£»
¢Śµ±k£¾0Ź±£¬£ØPA+AO£©£ØPB©BO£©µÄÖµĖękµÄŌö“ó¶ųŌö“ó£»
¢Ūµ±k=- ![]() Ź±£¬BP2=BOBA£»
Ź±£¬BP2=BOBA£»
¢Ü”÷PABĆ껿µÄ×īŠ”ÖµĪŖ ![]() £®
£®
ĘäÖŠÕżČ·µÄŹĒ £® £ØŠ“³öĖłÓŠÕżČ·Ėµ·ØµÄŠņŗÅ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖÅ×ĪļĻßy= ![]() x2+bx+c£Øb£¬cĪŖ³£Źż£©µÄ¶„µćĪŖP£¬µČŃüÖ±½ĒČż½ĒŠĪABCµÄ¶„µćAµÄ×ų±źĪŖ£Ø0£¬©1£©£¬CµÄ×ų±źĪŖ£Ø4£¬3£©£¬Ö±½Ē¶„µćBŌŚµŚĖÄĻóĻŽ£®
x2+bx+c£Øb£¬cĪŖ³£Źż£©µÄ¶„µćĪŖP£¬µČŃüÖ±½ĒČż½ĒŠĪABCµÄ¶„µćAµÄ×ų±źĪŖ£Ø0£¬©1£©£¬CµÄ×ų±źĪŖ£Ø4£¬3£©£¬Ö±½Ē¶„µćBŌŚµŚĖÄĻóĻŽ£®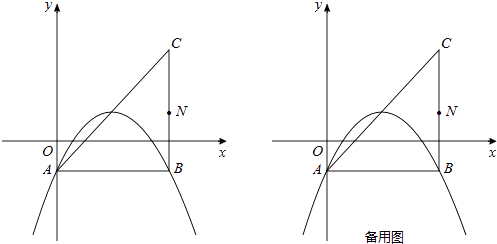
£Ø1£©ČēĶ¼£¬ČōøĆÅ×ĪļĻß¹żA£¬BĮ½µć£¬ĒóøĆÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©Ę½ŅĘ£Ø1£©ÖŠµÄÅ×ĪļĻߣ¬Ź¹¶„µćPŌŚÖ±ĻßACÉĻ»¬¶Æ£¬ĒŅÓėAC½»ÓŚĮķŅ»µćQ£®
£Øi£©ČōµćMŌŚÖ±ĻßACĻĀ·½£¬ĒŅĪŖĘ½ŅĘĒ°£Ø1£©ÖŠµÄÅ×ĪļĻßÉĻµÄµć£¬µ±ŅŌM”¢P”¢QČżµćĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬Ēó³öĖłÓŠ·ūŗĻĢõ¼žµÄµćMµÄ×ų±ź£»
£Øii£©Č”BCµÄÖŠµćN£¬Į¬½ÓNP£¬BQ£®ŹŌĢ½¾æ ![]() ŹĒ·ń“ęŌŚ×ī“óÖµ£æČō“ęŌŚ£¬Ēó³öøĆ×ī“óÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ŹĒ·ń“ęŌŚ×ī“óÖµ£æČō“ęŌŚ£¬Ēó³öøĆ×ī“óÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬Į¬½ÓBD£¬µćOŹĒBDµÄÖŠµć£¬ČōM”¢NŹĒ±ßADÉĻ²»ÓėA”¢DÖŲŗĻµÄĮ½µć£¬Į¬½ÓMO”¢NO£¬²¢·Ö±šŃÓ³¤½»BC±ßÓŚM”䔢N”äĮ½µć£¬ŌņĶ¼ÖŠµÄČ«µČČż½ĒŠĪÓŠ_____¶Ō£®
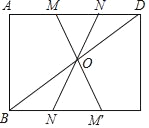
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
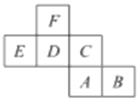
”¾ĢāÄæ”æČēĶ¼ŹĒŅ»øöÕż·½ĢåµÄÕ¹æŖĶ¼£¬±ź×¢ĮĖ×ÖÄø![]() £¬
£¬![]() µÄĆę·Ö±šŹĒÕż·½ĢåµÄÕżĆęŗĶµ×Ćę£¬ĘäĖūĆę·Ö±šÓĆ×ÖÄø
µÄĆę·Ö±šŹĒÕż·½ĢåµÄÕżĆęŗĶµ×Ćę£¬ĘäĖūĆę·Ö±šÓĆ×ÖÄø![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ±ķŹ¾£®ŅŃÖŖ
±ķŹ¾£®ŅŃÖŖ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £®
£®
(1)Čē¹ūÕż·½ĢåµÄ×óĆęÓėÓŅĆęĖł±ź×¢×ÖÄø“ś±ķµÄ“śŹżŹ½µÄÖµĻąµČ£¬Ēó³ö![]() µÄÖµ£»
掙术
(2)Čē¹ūÕżĆę×ÖÄø![]() “ś±ķµÄ“śŹżŹ½Óė¶ŌĆę×ÖÄø“ś±ķµÄ“śŹżŹ½µÄÖµĻąµČ£¬ĒŅ
“ś±ķµÄ“śŹżŹ½Óė¶ŌĆę×ÖÄø“ś±ķµÄ“śŹżŹ½µÄÖµĻąµČ£¬ĒŅ![]() ĪŖÕūŹż£¬ĒóÕūŹż
ĪŖÕūŹż£¬ĒóÕūŹż![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖ滜ĻµĶ³¶ŌĪļžµÄ¹ÜĄķĶس£²ÉÓĆŹ÷ŠĪÄæĀ¼½į¹¹£¬·½Ź½ČēĶ¼£¬ŌŚŅ»øöøłÄæĀ¼ĻĀ½ØĮ¢ČōøÉ×ÓÄæĀ¼(ÕāĄļ³ĘµŚŅ»²ćÄæĀ¼)£¬Ćæøö×ÓÄæĀ¼ÓÖæÉ×÷ĪŖøøÄæĀ¼£¬ĻņĻĀ¼ĢŠų½ØĮ¢Ęä×ÓÄæĀ¼(ÕāĄļ³ĘµŚ¶ž²ćÄæĀ¼)£¬ŅĄ“Ī½ųŠŠ£¬æÉ““½Ø¶ą²ćÄæĀ¼£®ĻÖŌŚŅ»øłÄæĀ¼ĻĀ½ØĮ¢ĮĖĖIJćÄæĀ¼£¬²¢ĒŅĆæŅ»øöøøÄæĀ¼ĻĀµÄ×ÓÄæĀ¼µÄøöŹż¶¼ĻąĶ¬£¬¶¼µČÓŚøłÄæĀ¼ĻĀÄæĀ¼µÄøöŹż£®ŅŃÖŖµŚČż²ćÄæĀ¼¹²ÓŠ343øö£¬ĒóÕāŅ»øłÄæĀ¼ĻĀµÄĖłÓŠÄæĀ¼µÄøöŹż£®
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģkx2©£Ø4k+1£©x+3k+3£½0£ØkŹĒÕūŹż£©£®
£Ø1£©ĒóÖ¤£ŗ·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£»
£Ø2£©Čō·½³ĢµÄĮ½øöŹµŹżøł¶¼ŹĒÕūŹż£¬ĒókµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com