
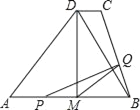
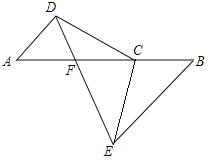
”¾ĢāÄæ”æČēĶ¼£¬MĪŖµČŃü”÷ABDµÄµ×ABµÄÖŠµć£¬¹żD×÷DC”ĪAB£¬Į¬½įBC£»AB=8cm£¬DM=4cm£¬DC=1cm£¬¶ÆµćP×ŌAµć³ö·¢£¬ŌŚABÉĻŌČĖŁŌĖ¶Æ£¬¶ÆµćQ×ŌµćB³ö·¢£¬ŌŚÕŪĻßBC©CDÉĻŌČĖŁŌĖ¶Æ£¬ĖŁ¶Č¾łĪŖ1cm/s£¬µ±ĘäÖŠŅ»øö¶Æµćµ½“ļÖÕµćŹ±£¬ĖüĆĒĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ÉčµćPŌĖ¶Æt£Øs£©Ź±£¬”÷MPQµÄĆ껿ĪŖS£Ø²»Äܹ¹³É”÷MPQµÄ¶Æµć³żĶā£©£®
£Ø1£©t£Øs£©ĪŖŗĪÖµŹ±£¬µćQŌŚBCÉĻŌĖ¶Æ£¬t£Øs£©ĪŖŗĪÖµŹ±£¬µćQŌŚCDÉĻŌĖ¶Æ£»
£Ø2£©ĒóSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©µ±tĪŖŗĪÖµŹ±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ¶ąÉŁ£æ
£Ø4£©µ±µćQŌŚCDÉĻŌĖ¶ÆŹ±£¬Ö±½ÓŠ“³ötĪŖŗĪÖµŹ±£¬”÷MPQŹĒµČŃüČż½ĒŠĪ£®
”¾“š°ø”æ£Ø1£©µ±0£¼t”Ü5ĒŅt”Ł4£Øs£©Ź±£¬µćQŌŚBCÉĻŌĖ¶Æ£»µ±5”Üt”Ü6£Øs£©Ź±£¬µćQŌŚCDÉĻŌĖ¶Æ£»£Ø2£©µ±0£¼t£¼4Ź±S=©![]() t2+
t2+![]() £»µ±4£¼t”Ü5Ź±£¬S=
£»µ±4£¼t”Ü5Ź±£¬S=![]() t2©
t2©![]() £»µ±5£¼t”Ü6Ź±£¬S=2t©8£»£Ø3£©µ±t=6Ź±£¬SČ”µ½×ī“óÖµ£¬×ī“óÖµĪŖ4£»£Ø4£©µ±t=
£»µ±5£¼t”Ü6Ź±£¬S=2t©8£»£Ø3£©µ±t=6Ź±£¬SČ”µ½×ī“óÖµ£¬×ī“óÖµĪŖ4£»£Ø4£©µ±t=![]() ĆėŹ±£¬”÷MPQŹĒµČŃüČż½ĒŠĪ£®
ĆėŹ±£¬”÷MPQŹĒµČŃüČż½ĒŠĪ£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©¹żµćC×÷CE”ĶAB£¬“¹×ćĪŖE£¬æÉŅŌÖ¤µ½ĖıߊĪDCEMŹĒ¾ŲŠĪ£¬“Ó¶ųæÉŅŌĒó³ö![]() µÄ³¤£¬Č»ŗóæ¼ĀĒ²»Äܹ¹³É
µÄ³¤£¬Č»ŗóæ¼ĀĒ²»Äܹ¹³É![]() µÄĒéæö£¬¼“æɽā¾öĪŹĢā£®
µÄĒéæö£¬¼“æɽā¾öĪŹĢā£®
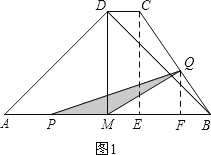
£Ø2£©ÓÉÓŚµćPŌŚµćMµÄĮ½±ßŹ±PMµÄ±ķ“ļŹ½²»Ķ¬£¬µćQŌŚĻ߶ĪBCŗĶDCÉĻŹ±µćQµ½PMµÄ¾ąĄėµÄ±ķ“ļŹ½²»Ķ¬£¬Ņņ“ĖŠč·ÖČżÖÖĒéæöĢÖĀŪ£¬ČēĶ¼1”¢2”¢3ĖłŹ¾£¬Č»ŗóÖ»ŠčÓĆtµÄ“śŹżŹ½±ķŹ¾³öPM¼°Ęä±ßÉĻµÄøߣ¬¾ĶæÉĒó³öSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø3£©ĄūÓƶž“ĪŗÆŹżŗĶŅ»“ĪŗÆŹżµÄŠŌÖŹ¶Ō£Ø2£©ÖŠµÄČżÖÖĒéæö½ųŠŠ·ÖĪö£¬¼“æɽā¾öĪŹĢā£®
£Ø4£©Ņ×Ö¤QM”ŁMP£¬QP”ŁMP.Čō![]() ŹĒµČŃüČż½ĒŠĪ£¬Ö»ÄÜŹĒ
ŹĒµČŃüČż½ĒŠĪ£¬Ö»ÄÜŹĒ![]() ÓÉ
ÓÉ![]() æÉµĆ£ŗ
æÉµĆ£ŗ ![]() ŌŁÓÉ
ŌŁÓÉ![]() æɵƵ½¹ŲÓŚtµÄ·½³Ģ£¬½āÕāøö·½³Ģ¼“æɽā¾öĪŹĢā£®
æɵƵ½¹ŲÓŚtµÄ·½³Ģ£¬½āÕāøö·½³Ģ¼“æɽā¾öĪŹĢā£®
ŹŌĢā½āĪö£ŗ(1)¹żµćC×÷CE”ĶAB£¬“¹×ćĪŖE£¬ČēĶ¼1£¬
”ßDA=DB£¬AM=BM£¬
”ąDM”ĶAB.
”ßCE”ĶAB£¬
”ą![]()
”ąCE”ĪDM.
”ßDC”ĪME,CE”ĪDM, ![]()
”ąĖıߊĪDCEMŹĒ¾ŲŠĪ£¬
”ąCE=DM=4£¬ME=DC=1.
ӧAM=BM,AB=8,
”ąAM=BM=4.
”ąBE=BMME=3.
ӧ![]()
”ąCB=5.
”ßµ±t=4Ź±£¬µćPÓėµćMÖŲŗĻ£¬²»Äܹ¹³É”÷MPQ£¬
”ąt”Ł4.
”ąµ±![]() ĒŅt”Ł4(s)Ź±,µćQŌŚBCÉĻŌĖ¶Æ;µ±
ĒŅt”Ł4(s)Ź±,µćQŌŚBCÉĻŌĖ¶Æ;µ±![]() (s)Ź±£¬µćQŌŚCDÉĻŌĖ¶Æ.
(s)Ź±£¬µćQŌŚCDÉĻŌĖ¶Æ.
(2)¢Łµ±0<t<4Ź±£¬µćPŌŚĻ߶ĪAMÉĻ£¬µćQŌŚĻ߶ĪBCÉĻ£¬
¹żµćQ×÷QF”ĶAB£¬“¹×ćĪŖF£¬ČēĶ¼1£¬
”ßQF”ĶAB£¬CE”ĶAB£¬
”ą![]()
”ąQF”ĪCE.
”ą”÷QFB”×”÷CEB.
”ą![]()
”ßCE=4£¬BC=5£¬BQ=t£¬
”ą![]()
”ą![]()
”ßPM=AMAP=4t£¬
”ą![]()
¢Śµ±![]() Ź±£¬µćPŌŚĻ߶ĪBMÉĻ£¬µćQŌŚĻ߶ĪBCÉĻ£¬
Ź±£¬µćPŌŚĻ߶ĪBMÉĻ£¬µćQŌŚĻ߶ĪBCÉĻ£¬
¹żµćQ×÷QF”ĶAB£¬“¹×ćĪŖF£¬ČēĶ¼2£¬
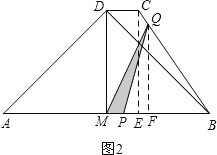
”ßQF”ĶAB,CE”ĶAB,
”ą![]()
”ąQF”ĪCE.
”ą”÷QFB”×”÷CEB.
”ą![]()
”ßCE=4£¬BC=5£¬BQ=t£¬
”ą![]()
”ą![]()
”ßPM=APAM=t4£¬
”ą![]()
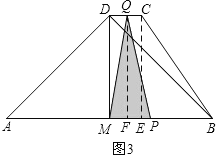
¢Ūµ±![]() Ź±£¬µćPŌŚĻ߶ĪBMÉĻ£¬µćQŌŚĻ߶ĪDCÉĻ£¬
Ź±£¬µćPŌŚĻ߶ĪBMÉĻ£¬µćQŌŚĻ߶ĪDCÉĻ£¬
¹żµćQ×÷QF”ĶAB£¬“¹×ćĪŖF£¬ČēĶ¼3£¬
“ĖŹ±QF=DM=4.
”ßPM=APAM=t4£¬
”ą![]()
×ŪÉĻĖłŹö£ŗµ±![]() µ±
µ±![]() Ź±,
Ź±, ![]() µ±
µ±![]() Ź±£¬S=2t8.
Ź±£¬S=2t8.
(3)¢Łµ±0<t<4Ź±, ![]()
”ß![]() 0<2<4£¬
0<2<4£¬
”ąµ±t=2Ź±,SČ”µ½×ī“óÖµ,×ī“óÖµĪŖ![]()
¢Śµ±![]() Ź±,
Ź±, ![]() ¶Ō³ĘÖįĪŖx=2.
¶Ō³ĘÖįĪŖx=2.
ӧ![]()
”ąµ±x>2Ź±£¬SĖę×ÅtµÄŌö“ó¶ųŌö“ó£¬
”ąµ±t=5Ź±,SČ”µ½×ī“óÖµ,×ī“óÖµĪŖ![]()
¢Ūµ±![]() Ź±£¬S=2t8.
Ź±£¬S=2t8.
”ß2>0£¬
”ąSĖę×ÅtµÄŌö“ó¶ųŌö“ó,
”ąµ±t=6Ź±£¬SČ”µ½×ī“óÖµ£¬×ī“óÖµĪŖ2”Į68=4.
×ŪÉĻĖłŹö£ŗµ±t=6Ź±£¬SČ”µ½×ī“óÖµ£¬×ī“óÖµĪŖ4.
(4)µ±µćQŌŚCDÉĻŌĖ¶Æ¼“![]() Ź±£¬ČēĶ¼3£¬
Ź±£¬ČēĶ¼3£¬
ŌņÓŠ![]()
![]() £¬¼“
£¬¼“![]()
”ßMP=t4<64£¬¼“MP<2£¬
”ąQM”ŁMP£¬QP”ŁMP.
Čō”÷MPQŹĒµČŃüČż½ĒŠĪ£¬ŌņQM=QP.
”ßQM=QP£¬QF”ĶMP£¬
”ąMF=PF=12MP.
”ßMF=DQ=5+1t=6t£¬MP=t4£¬
”ą![]()
½āµĆ£ŗ ![]()
”ąµ±t=![]() ĆėŹ±£¬”÷MPQŹĒµČŃüČż½ĒŠĪ.
ĆėŹ±£¬”÷MPQŹĒµČŃüČż½ĒŠĪ.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā·½³Ģ![]()
½ā:·½³ĢĮ½±ßĶ¬Ź±³ĖŅŌ(x+2)(x-2)”(A)
(x+2)(x-2)![]()
»Æ¼ņµĆ:x-2+4x=2(x+2)”.. (B)
Č„ĄØŗÅ”¢ŅĘĻīµĆ:x+4x-2x=4+2”(C)
½āµĆ:x=2”..(D)
Ō·½³ĢµÄ½āŹĒx=2”.(E)
ĪŹĢā:¢ŁÉĻŹö½āĢā¹ż³ĢµÄ“ķĪóŌŚµŚ____²½,ĘäŌŅņŹĒ_____¢ŚøĆ²½øÄÕżĪŖ:
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠÓŠĮ½¼Ņ³ö×ā³µ¹«Ė¾£¬ŹÕ·Ń±ź×¼²»Ķ¬£¬¼×¹«Ė¾ŹÕ·Ń±ź×¼ĪŖ£ŗĘš²½¼Ū8ŌŖ£¬³¬¹ż3Ē§Ć×ŗ󣬳¬¹żµÄ²æ·Ö°“ÕÕĆæĒ§Ć×1.5ŌŖŹÕ·Ń£»ŅŅ¹«Ė¾ŹÕ·Ń±ź×¼ĪŖ£ŗĘš²½¼Ū11ŌŖ£¬³¬¹ż3Ē§Ć×ŗ󣬳¬¹żµÄ²æ·Ö°“ÕÕĆæĒ§Ć×1.2ŌŖŹÕ·Ń£¬³µĮ¾ŠŠŹ»![]() Ē§Ć×£¬±¾ĢāÖŠ
Ē§Ć×£¬±¾ĢāÖŠ![]() Č”ÕūŹż£¬²»×ć1Ē§Ć×µÄĀ·³Ģ°“1Ē§Ć×¼Ę·Ń£¬øł¾ŻÉĻŹöÄŚČŻ£¬Ķź³ÉŅŌĻĀĪŹĢā£ŗ
Č”ÕūŹż£¬²»×ć1Ē§Ć×µÄĀ·³Ģ°“1Ē§Ć×¼Ę·Ń£¬øł¾ŻÉĻŹöÄŚČŻ£¬Ķź³ÉŅŌĻĀĪŹĢā£ŗ
£Ø1£©µ±![]() Ź±£¬ŅŅ¹«Ė¾±Č¼×¹«Ė¾¹ó______ŌŖ£»
Ź±£¬ŅŅ¹«Ė¾±Č¼×¹«Ė¾¹ó______ŌŖ£»
£Ø2£©µ±![]() £¬ĒŅ
£¬ĒŅ![]() ĪŖÕūŹżŹ±£¬¼×ŅŅĮ½¹«Ė¾µÄŹÕ·Ń·Ö±šŹĒ¶ąÉŁ£æ£Ø½į¹ūÓĆ»Æ¼ņŗóµÄŗ¬
ĪŖÕūŹżŹ±£¬¼×ŅŅĮ½¹«Ė¾µÄŹÕ·Ń·Ö±šŹĒ¶ąÉŁ£æ£Ø½į¹ūÓĆ»Æ¼ņŗóµÄŗ¬![]() µÄŹ½×Ó±ķŹ¾£©;
µÄŹ½×Ó±ķŹ¾£©;
£Ø3£©µ±ŠŠŹ»Ā·³ĢĪŖ18Ē§Ć׏±£¬ÄļŅ¹«Ė¾µÄ·ŃÓĆøü±ćŅĖ£æ±ćŅĖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”ÓūÕŠĘøŅ»ĆūŌ±¹¤£¬ĻÖÓŠ¼×”¢ŅŅĮ½ČĖ¾ŗĘø£®Ķعż¼ĘĖ滜”¢ÓļŃŌŗĶÉĢĘ·ÖŖŹ¶ČżĻī²āŹŌ£¬ĖūĆĒø÷×Ō³É¼Ø£Ø°Ł·ÖÖĘ£©ČēĻĀ±ķĖłŹ¾£ŗ
Ó¦ŹŌÕß | ¼ĘĖ滜 | ÓļŃŌ | ÉĢĘ·ÖŖŹ¶ |
¼× | 70 | 50 | 80 |
ŅŅ | 60 | 60 | 80 |
£Ø1£©ČōÉĢ³”ŠčŅŖÕŠĘøøŗŌš½«ÉĢĘ·²š×°ÉĻ¼ÜµÄČĖŌ±£¬¶Ō¼ĘĖ滜”¢ÓļŃŌŗĶÉĢĘ·ÖŖŹ¶·Ö±šø³ČØ2£¬3£¬5£¬¼ĘĖćĮ½ĆūÓ¦ŹŌÕßµÄĘ½¾ł³É¼Ø£®“ӳɼØæ“£¬Ó¦øĆĀ¼Č”Ė£æ
£Ø2£©ČōÉĢ³”ŠčŅŖÕŠĘøµēÄŌŹÕŅųŌ±£¬¼ĘĖ滜”¢ÓļŃŌŗĶÉĢĘ·ÖŖŹ¶³É¼Ø·Ö±šÕ¼50%£¬30%£¬20%£¬¼ĘĖćĮ½ĆūÓ¦ŹŌÕßµÄĘ½¾ł³É¼Ø£®“ӳɼØæ“£¬Ó¦øĆĀ¼Č”Ė£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”µŚŅ»“ĪÓĆ11000ŌŖ¹ŗ½ųijæīʓװ»śĘ÷ČĖ½ųŠŠĻśŹŪ£¬ŗÜæģĻśŹŪŅ»æÕ£¬ÉĢ¼ŅÓÖÓĆ24000ŌŖµŚ¶ž“Ī¹ŗ½ųĶ¬æī»śĘ÷ČĖ£¬Ėł¹ŗ½ųŹżĮæŹĒµŚŅ»“ĪµÄ2±¶£¬µ«µ„¼Ū¹óĮĖ10ŌŖ£®
£Ø1£©ĒóøĆÉĢ¼ŅµŚŅ»“Ī¹ŗ½ų»śĘ÷ČĖ¶ąÉŁøö£æ
£Ø2£©ČōĖłÓŠ»śĘ÷ČĖ¶¼°“ĻąĶ¬µÄ±ź¼ŪĻśŹŪ£¬ŅŖĒóČ«²æĻśŹŪĶź±ĻµÄĄūČóĀŹ²»µĶÓŚ20%£Ø²»æ¼ĀĒĘäĖüŅņĖŲ£©£¬ÄĒĆ“Ćæøö»śĘ÷ČĖµÄ±ź¼ŪÖĮÉŁŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬CŹĒABÉĻŅ»µć£¬µćD£¬E·Ö±šŌŚABĮ½²ą£¬AD”ĪBE£¬ĒŅAD£½BC£¬BE£½AC£®
£Ø1£©ĒóÖ¤£ŗCD£½CE£»
£Ø2£©Į¬½ÓDE£¬½»ABÓŚµćF£¬²ĀĻė”÷BEFµÄŠĪד£¬²¢øųÓčÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
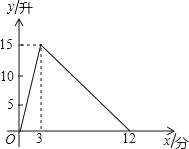
”¾ĢāÄæ”æŅ»øöÓŠ½ųĖ®¹ÜÓė³öĖ®¹ÜµÄČŻĘ÷£¬“ÓijŹ±æĢæŖŹ¼µÄ3·ÖÄŚÖ»½ųĖ®²»³öĖ®£¬ŌŚĖęŗóµÄ9·ÖÄŚ¼Č½ųĖ®ÓÖ³öĖ®£¬Ćæ·ÖµÄ½ųĖ®ĮæŗĶ³öĖ®Į涼ŹĒ³£Źż£®ČŻĘ÷ÄŚµÄĖ®Įæy£Øµ„Ī»£ŗÉż£©ÓėŹ±¼äx£Øµ„Ī»£ŗ·Ö£©Ö®¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾£®
¢Łµ±0”Üx”Ü3Ź±£¬ĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®
¢Ś3£¼x”Ü12Ź±£¬ĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®
¢Ūµ±ČŻĘ÷ÄŚµÄĖ®Įæ“óÓŚ5ÉżŹ±£¬ĒóŹ±¼äxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
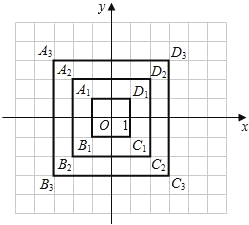
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŗį×ų±ź”¢×Ż×ų±ź¶¼ĪŖÕūŹżµÄµć³ĘĪŖÕūµć£®ĒėÄć¹Ū²ģĶ¼ÖŠÕż·½ŠĪA1B1C1D1£¬A2B2C2D2£¬A3B3C3D3”ĆæøöÕż·½ŠĪĖÄĢõ±ßÉĻµÄÕūµćµÄøöŹż£®°““Ė¹ęĀÉĶĘĖć³öÕż·½ŠĪA10B10C10D10ĖÄĢõ±ßÉĻµÄÕūµć¹²ÓŠ______øö£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹ÉĆńÉĻŠĒĘŚĪåĀņ½ųij¹«Ė¾¹Éʱ1000¹É£¬Ćæ¹É27ŌŖ£¬ĻĀ±ķĪŖ±¾ÖÜÄŚĆæČÕøĆ¹ÉʱµÄÕĒµųĒéæö£Øµ„Ī»£ŗŌŖ£©£ØÖÜĮł”¢ÖÜČÕŠŻÅĢ£©
ŠĒĘŚ | Ņ» | ¶ž | Čż | ĖÄ | Īå |
Ćæ¹É ÕĒµų | +4 | +4.5 | £1 | £1.5 | £4 |
£Ø1£©ŠĒĘŚĪåŹÕÅĢŹ±£¬Ćæ¹ÉŹĒ¶ąÉŁŌŖ£æ
£Ø2£©±¾ÖÜÄŚ×īøß¼ŪŹĒĆæ¹É¶ąÉŁŌŖ£æ×īµĶ¼ŪŹĒĆæ¹É¶ąÉŁŌŖ£æ
£Ø3£©ŅŃÖŖøĆ¹ÉĆńĀņ½ų¹ÉʱŹ±ø¶ĮĖ0.15%µÄŹÖŠų·Ń£¬Āō³öŹ±Ščø¶³É½»¶ī0.15%µÄŹÖŠų·ŃŗĶ0.1%µÄ½»Ņ×Ė°£¬ČōøĆ¹ÉĆńŌŚŠĒĘŚĪåŹÕÅĢĒ°½«Č«²æ¹ÉʱĀō³ö£¬ĖūµÄŹÕŅęĒéæöČēŗĪ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com