
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π);
(4)求出(2)△A2BC2的面积是多少.

【答案】(1)画图见解析,点A1的坐标为(2,﹣4);(2)画图见解析;(3)![]() π;(4)3.5.
π;(4)3.5.
【解析】
(1)根据关于x轴对称的点的坐标特征,写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质,画出点A、C的对应点A2、C2,则可得到△A2BC2;
(3)C点旋转到C2点所经过的路径是以B点为圆心,BC为半径,圆心角为90°的弧,然后根据弧长公式计算即可;
(4)利用一个矩形的面积分别减去三个三角形的面积可计算出△A2BC2的面积.
(1)如图,△A1B1C1为所作,点A1的坐标为(2,﹣4);
(2)如图,△A2BC2为所作;
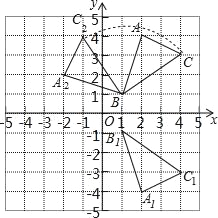
(3)![]() ,
,
所以C点旋转到C2点所经过的路径长![]()
(4)△A2BC2的面积![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】恒昌路是一条东西走向的马路,有市场、医院、车站、学校四家公共场所。已知市场在医院东200米,车站在市场东150米,医院在学校东450米。若将马路近似的看成一条直线,以医院为原点,向东方向为正方向,用1个单位长度表示100米,
(1)在数轴上表示出四家公共场所的位置;
![]()
(2)列式计算学校与车站之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.如图,已知AB∥CD,∠B=∠C,
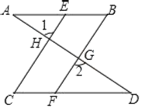
求证:∠1=∠2.
证明:∵AB∥CD(已知)
∴∠B= ( ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ ( )
∴∠2= (两直线平行,同位角相等)
∵∠1= ( )
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:(3x﹣6)(x2﹣![]() )﹣6x(
)﹣6x(![]() x2﹣x﹣6),其中x=﹣
x2﹣x﹣6),其中x=﹣![]() .
.
(2)已知y2﹣5y+3=0,求2(y﹣1)(2y﹣1)﹣2(y+1)2+7的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a度/秒,灯B转动的速度是b度/秒,且a,b满足|a﹣3b﹣1|+(a+b﹣5)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a,b的值;
(2)若两灯同时转动,经过42秒,两灯射出的光束交于C,求此时∠ACB的度数;
(3)若灯B射线先转动10秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com