
分析 (1)求出方程组1的解即可;
(2)观察一系列方程组的解特征,归纳总结得到一般性规律即可;
(3)利用加减消元法求出方程组的解,验证即可.
解答 解:(1)$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$;
(2)方程组n$\left\{\begin{array}{l}{x+y=1}\\{x-ny={n}^{2}}\end{array}\right.$它的解是$\left\{\begin{array}{l}{x=n}\\{y=-(n-1)}\end{array}\right.$;
故答案为:$\left\{\begin{array}{l}{x+y=1}\\{x-ny={n}^{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=n}\\{y=-(n-1)}\end{array}\right.$;
( 通过观察分析,得方程组中第1个方程不变,只是第2个方程中y的系数依次变为-1,-2,-3,…,-n,第2个方程的常数规律是n2.
它们解的规律是x=1,2,3,…,n.
相应的y=0,-1,-2,-(n-1).)
(3)因为$\left\{\begin{array}{l}{x=5}\\{y=-4}\end{array}\right.$是方程组$\left\{\begin{array}{l}{x+y=1}\\{x-ay=25}\end{array}\right.$的解,
所以有5-a×(-4)=25,
解得a=5,
即原方程组为$\left\{\begin{array}{l}{x+y=1}\\{x-5y=25}\end{array}\right.$
所以该方程组符合(2)中的规律.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
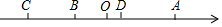 如图,在数轴上,点A表示的数是50,点C和点A到原点O距离相等,点D在点A的左侧距离A点40个单位长度,点B是线段CD的中点.
如图,在数轴上,点A表示的数是50,点C和点A到原点O距离相等,点D在点A的左侧距离A点40个单位长度,点B是线段CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
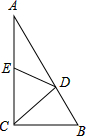 如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.
如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2=0 | B. | ax2+bx+c=0(a,b,c均为常数) | ||
| C. | x2+y=5 | D. | x3+$\frac{2}{x}$+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com