
如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作y轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

解:(1)由A(4,0),可知OA=4,
∵OA=OC=4OB,
∴OA=OC=4,OB=1,
∴C(0,4),B(﹣1,0).
设抛物线的解析式是y=ax2+bx+x,
则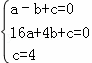 ,
,
解得: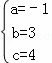 ,
,
则抛物线的解析式是:y=﹣x2+3x+4;
(2)存在.
第一种情况,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵∠ACP1=90°,
∴∠MCP1+∠ACO=90°.
∵∠ACO+∠OAC=90°,
∴∠MCP1=∠OAC.
∵OA=OC,
∴∠MCP1=∠OAC=45°,
∴∠MCP1=∠MP1C,
∴MC=MP1,
设P(m,﹣m2+3m+4),则m=﹣m2+3m+4﹣4,
解得:m1=0(舍去),m2=2.
∴﹣m2+3m+4=6,
即P(2,6).
第二种情况,当点A为直角顶点时,过A作AP2,AC交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP交y轴于点F.
∴P2N∥x轴,
由∠CAO=45°,
∴∠OAP=45°,
∴∠FP2N=45°,AO=OF.
∴P2N=NF,
设P2(n,﹣n2+3n+4),则n=(﹣n2+3n+4)﹣1,
解得:n1=﹣2,n2=4(舍去),
∴﹣n2+3n+4=﹣6,
则P2的坐标是(﹣2,﹣6).
综上所述,P的坐标是(2,6)或(﹣2,﹣6);

(3)连接OD,由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短.
由(1)可知,在直角△AOC中,OC=OA=4,
则AC= =4
=4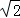 ,
,
根据等腰三角形的性质,D是AC的中点.
又∵DF∥OC,
∴DF= OC=2,
OC=2,
∴点P的纵坐标是2.
则﹣x2+3x+1=2,
解得:x= ,
,
∴当EF最短时,点P的坐标是:(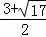 ,0)或(
,0)或( ,0).
,0).


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
地球的表面积约为511000000km2,用科学记数法表示正确的是( )

|
| A. | 5.11×1010km2 | B. | 5.11×108km2 | C. | 51.1×107km2 | D. | 0.511×109km2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 .
.
以上结论中,你认为正确的有( )个.

|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
2011年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,丙绘制了不完整的两种统计图.
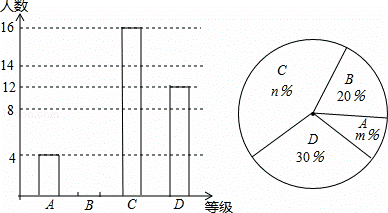
根据图中提供的信息,回答下列问题:
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形的圆心角为 度;
(3)学校欲从或A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求或A等级的小明参加市比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,□ABCD的顶点A(0,0),B(5,0),D(2,3),则顶点C的坐标是【 】
A、(3,7) B、(5,3) C、(7,3) D、(8,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com