
如图所示,一架投影机插入胶片后图像可投到屏幕上. 已知胶片与屏幕平行,A点为光源,与胶片BC的距离为0.1米,胶片的高BC为0.038米,若需要投影后的图像DE高1.9米,则投影机光源离屏幕大约为( )
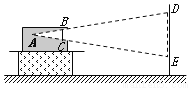
A. 6米 B. 5米 C. 4米 D. 3米
B 【解析】试题解析:如图所示,过A作AG⊥DE于G,交BC与F 因为BC∥DE,所以△ABC∽△ADE,AG⊥BC,AF=0.1m,设AG=h, 则: ,即,解得:h=5m. 故选B.科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第3章 一元一次方程 单元测试卷 题型:单选题
图①为一正面白色、反面灰色的长方形纸片.今沿虚线剪下分成甲、乙两长方形纸片,并将甲纸片反面朝上粘贴于乙纸片上,形成一张白、灰相间的长方形纸片,如图②所示.若图②中白色与灰色区域的面积比为8∶3,图②纸片的面积为33,则图①纸片的面积为( )

A.  B.
B. 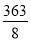 C. 42 D. 44
C. 42 D. 44
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第25章 概率初步 单元测试卷 题型:填空题
如图,有五张背面完全相同的纸质卡片,其正面分别标有数:6、 、
、 、-2、
、-2、 .将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数比3小的概率是___________
.将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数比3小的概率是___________

查看答案和解析>>
科目:初中数学 来源:安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型:解答题
请你用四块如图1所示的瓷砖图案为“基本单位”, 在图2、图3中分别设计出一个正方形的地板图案,使拼铺的图案成轴对称图形或中心对称图形. (要求:两种拼法各不相同,所画图案阴影部分用斜线表示.)

查看答案和解析>>
科目:初中数学 来源:安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型:填空题
某商场为了解本商场的服务质量,随机调查了来本商场消费的200名顾客,调查的结果绘制成如图所示的统计图. 根据统计图所给出的信息,这200名顾客中对该商场的服务质量表示不满意的有_________人.

查看答案和解析>>
科目:初中数学 来源:安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型:单选题
如图所示的立方体,如果把它展开,可以是下列图形中的( )

A.  B.
B.  C.
C. 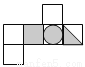 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十七章 达标检测卷 题型:解答题
在△ABC中,点D为BC上一点,连接AD,点E在BD上,且DE=CD,过点E作AB的平行线交AD于F,且EF=AC.如图,求证:∠BAD=∠CAD.
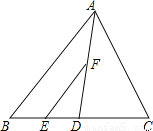
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十七章 达标检测卷 题型:单选题
如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为 时,△ABE与以D、M、N为顶点的三角形相似.

A.  B.
B. 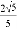 C.
C.  或
或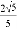 D.
D. 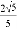 或
或
查看答案和解析>>
科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:填空题
用代数式表示:“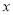 与
与 的和的平方”_________.
的和的平方”_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com