
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
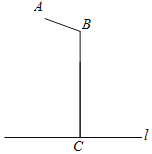
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
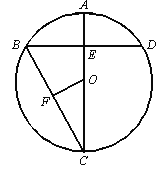
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() .抛物线的解析式为
.抛物线的解析式为![]() .
.
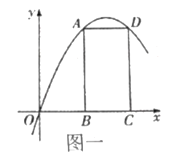
(1)如图一,若抛物线经过![]() ,
,![]() 两点,直接写出
两点,直接写出![]() 点的坐标 ;抛物线的对称轴为直线 ;
点的坐标 ;抛物线的对称轴为直线 ;
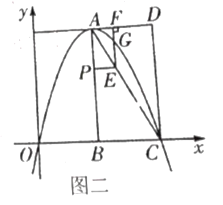
(2)如图二:若抛物线经过![]() 、
、![]() 两点,
两点,
①求抛物线的表达式.
②若点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() 交抛物线于点
交抛物线于点![]() .当线段
.当线段![]() 最长时,求点
最长时,求点![]() 的坐标;
的坐标;
(3)若![]() ,且抛物线与矩形
,且抛物线与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
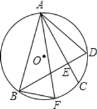
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
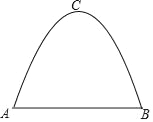
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.
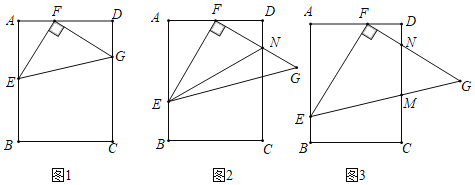
(1)如图1,当点G在CD上时,求证:△AEF≌△DFG;
(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:EN=AE+DN;
(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MNMD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
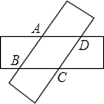
A. ∠ABC=∠ADC,∠BAD=∠BCDB. AB=BC
C. AB=CD,AD=BCD. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量x的取值范围是全体非零实数,因此函数图象会被y轴分成两部分;其次,分析解析式,得到y随x的变化趋势:当x>0时,随着x值的增大,y的值减小,且逐渐接近于零,随着x值的减小,y的值会越来越大,由此,可以大致画出
的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量x的取值范围是全体非零实数,因此函数图象会被y轴分成两部分;其次,分析解析式,得到y随x的变化趋势:当x>0时,随着x值的增大,y的值减小,且逐渐接近于零,随着x值的减小,y的值会越来越大,由此,可以大致画出![]() 在x>0时的部分图象,如图1所示.利用同样的方法,我们可以研究函数
在x>0时的部分图象,如图1所示.利用同样的方法,我们可以研究函数![]() 的图象与性质.
的图象与性质.
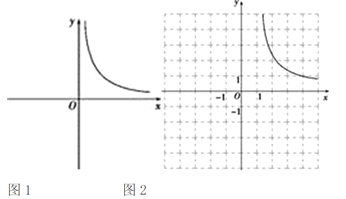
(1)该函数自变量x的取值范围_______________;
(2)通过分析解析式画出部分函数图象,如图2所示.请沿此思路在图2中完善函数图象的草图并标出此函数图象与y轴的交点A;(画出网格区域内的部分即可)
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() 有两个不相等的实数根,结合图象,直接写出实数a的取值范围: .
有两个不相等的实数根,结合图象,直接写出实数a的取值范围: .
查看答案和解析>>
科目:初中数学 来源: 题型:
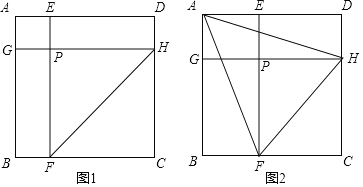
【题目】如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH、FH.
(1)如图1,若a=1,AE=AG=![]() ,求FH的值;
,求FH的值;
(2)如图2,若∠FAH=45°,证明:AG+AE=FH;
(3)若Rt△GBF的周长l=a,求矩形EPHD的面积S与l的关系(只写结果,不写过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com