
如图,在Rt 中,
中, ,以AC为直径的⊙O交AB于点D,E是BC的中点.
,以AC为直径的⊙O交AB于点D,E是BC的中点.
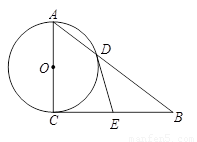
(1)求证:DE是⊙O的切线;
(2)过点E作EF⊥DE,交AB于点F.若AC=3,BC=4,求DF的长.
(1)证明见解析;(2)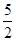 .
.
【解析】
试题分析:(1)连结OD,CD,求出DE=CE=BE,推出∠1+∠3=∠2+∠4,求出∠ACB=∠ODE=90°,根据切线的判定推出即可.
(2)根据勾股定理求出AB=5,解直角三角形得出cosB=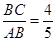 ,求出DE,推出∠EDF=∠B,解直角三角形求出即可.
,求出DE,推出∠EDF=∠B,解直角三角形求出即可.
试题解析:(1)证明:连结OD,CD.
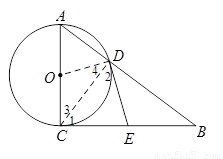
∵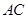 是直径,
是直径,
∴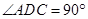 .
.
∴ .
.
∵E是BC的中点,
∴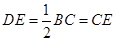 .
.
∴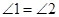 .
.
∵OC=OD,
∴∠3 =∠4 ,
∴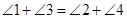 .
.
即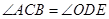 .
.
∵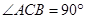 ,
,
∴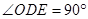 .
.
又∵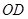 是半径,
是半径,
∴DE是⊙O的切线.
(2)解:在Rt△ABC中,
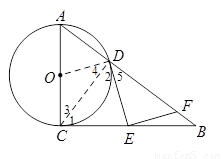
∵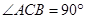 ,AC=3,BC=4,
,AC=3,BC=4,
∴AB=5. 4分
∴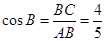 .
.
∵E是BC的中点,
∴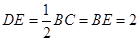 . 5分
. 5分
∴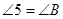 .
.
∴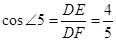 .
.
∴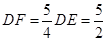 .
.
考点: 1.切线的判定;2.解直角三角形.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
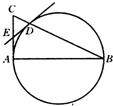 10、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
10、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长的速度向点
方向以每秒2个单位长的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长的速度向点
方向以每秒1个单位长的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() >0).过点
>0).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .(1)求证:四边形
.(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请直接写出
为直角三角形?请直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com