
【题目】已知如图,矩形OABC的长OA=![]() , 宽OC=1,将△AOC沿AC翻折得△APC.
, 宽OC=1,将△AOC沿AC翻折得△APC.
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)题(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.



【答案】(1)30°; (2)当x=0时,y=1,故C(0,1)在抛物线的图象上;(3)见解析
【解析】(1)根据OC、OA的长,可求得∠OCA=∠ACP=60°(折叠的性质),∠BCA=∠OAC=30°,由此可判断出∠PCB的度数.
(2)过P作PQ⊥OA于Q,在Rt△PAQ中,易知PA=OA=3,而∠PAO=2∠PAC=60°,即可求出AQ、PQ的长,进而可得到点P的坐标,将P、A坐标代入抛物线的解析式中,即可得到b、c的值,从而确定抛物线的解析式,然后将C点坐标代入抛物线的解析式中进行验证即可.
(3)根据抛物线的解析式易求得C、D、E点的坐标,然后分两种情况考虑:
①DE是平行四边形的对角线,由于CD∥x轴,且C在y轴上,若过D作直线CE的平行线,那么此直线与x轴的交点即为M点,而N点即为C点,D、E的坐标已经求得,结合平行四边形的性质即可得到点M的坐标,而C点坐标已知,即可得到N点的坐标;
②DE是平行四边形的边,由于A在x轴上,过A作DE的平行线,与y轴的交点即为N点,而M点即为A点;易求得∠DEA的度数,即可得到∠NAO的度数,已知OA的长,通过解直角三角形可求得ON的值,从而确定N点的坐标,而M点与A点重合,其坐标已知;
同理,由于C在y轴上,且CD∥x轴,过C作DE的平行线,也可找到符合条件的M、N点,解法同上.
解:(1)在Rt△OAC中,OA=![]() ,OC=1,则∠OAC=30°,∠OCA=60°;
,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP=![]() ,∠ACO=∠ACP=60°;
,∠ACO=∠ACP=60°;
∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°.
(2)过P作PQ⊥OA于Q;

Rt△PAQ中,∠PAQ=60°,AP=![]() ;
;
∴OQ=AQ=![]() ,PQ=
,PQ=![]() ,
,
所以P(![]() ,
, ![]() );
);
将P、A代入抛物线的表达式中,得: 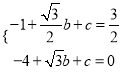 ,
,
解得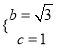 ;
;
即y=![]() x2+
x2+![]() x+1;
x+1;
当x=0时,y=1,故C(0,1)在抛物线的图象上.
(3)①若DE是平行四边形的对角线,点C在y轴上,CD平行x轴,
∴过点D作DM∥CE交x轴于M,则四边形EMDC为平行四边形,
把y=1代入抛物线解析式得点D的坐标为(![]() ,1)
,1)
把y=0代入抛物线解析式得点E的坐标为(![]() ,0)
,0)
∴M(![]() ,0);N点即为C点,坐标是N(0,1);
,0);N点即为C点,坐标是N(0,1);
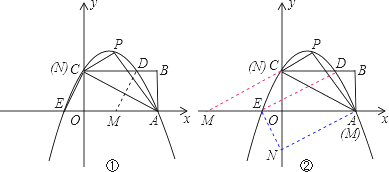
②若DE是平行四边形的边,
过点A作AN∥DE交y轴于N,四边形DANE是平行四边形,
∴DE=AN=![]() =
=![]() =2,
=2,
∴∠EAN=30°,∠DEA=30°,
∴M(![]() ,0),N(0,-1)
,0),N(0,-1)
同理过点C作CM∥DE交y轴于N,四边形CMDE是平行四边形,
∴M(-![]() ,0),N(0,1).
,0),N(0,1).
“点睛”此题考查了矩形的性质、图形的翻折变换、二次函数解析式的确定、平行四边形的判定和性质等知识,同时考查了分类讨论的数学思想,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度AB的长.

(2)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
①求证:四边形BCFE是菱形;
②在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图1,BF垂直CE于点F,交CD于点G,证明:AE=CG;
(2)如图2,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 ,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l外有一定点A,点A到直线l的距离是7cm,B是直线l上的任意一点,则线段AB的长度可能是________cm.(写出一个满足条件的值即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象经过点
的图象经过点![]() ,且当
,且当![]() 和
和![]() 时所对应的函数值相等.一次函数
时所对应的函数值相等.一次函数![]() 与二次函数
与二次函数![]() 的图象分别交于
的图象分别交于![]() ,
, ![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.

(![]() )求二次函数
)求二次函数![]() 的表达式.
的表达式.
(![]() )连接
)连接![]() ,求
,求![]() 的长.
的长.
(![]() )连接
)连接![]() ,
, ![]() 是线段
是线段![]() 得中点,将点
得中点,将点![]() 绕点
绕点![]() 旋转
旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,
, ![]() ,判断四边形
,判断四边形![]() 的性状,并证明你的结论.
的性状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com